


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-2-2020
Date: 2-1-2021
Date: 22-9-2020
|
Square line picking is the selection of pairs of points (corresponding to endpoints of a line segment) randomly placed inside a square. 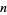 random line segments can be picked in a unit square in the Wolfram Language using the function RandomPoint[Rectangle[],
random line segments can be picked in a unit square in the Wolfram Language using the function RandomPoint[Rectangle[], 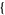 n, 2
n, 2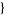 ].
].
Picking two points at random from the interior of a unit square, the average distance between them is the 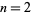 case of hypercube line picking, i.e.,
case of hypercube line picking, i.e.,
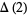 |
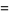 |
![1/(15)[sqrt(2)+2+5ln(1+sqrt(2))]](http://mathworld.wolfram.com/images/equations/SquareLinePicking/Inline7.gif) |
(1) |
 |
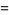 |
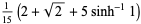 |
(2) |
 |
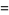 |
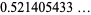 |
(3) |
(OEIS A091505).
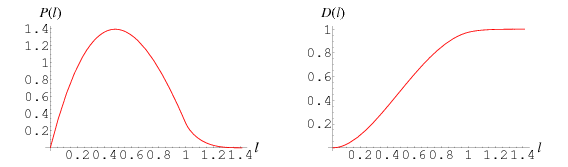
The exact probability function is given by
![P(l)={2l(l^2-4l+pi) for 0<=l<=1; 2l[4sqrt(l^2-1)-(l^2+2-pi)-4tan^(-1)(sqrt(l^2-1))] for 1<=l<=sqrt(2)](http://mathworld.wolfram.com/images/equations/SquareLinePicking/NumberedEquation1.gif) |
(4) |
(M. Trott, pers. comm., Mar. 11, 2004), and the corresponding distribution function by
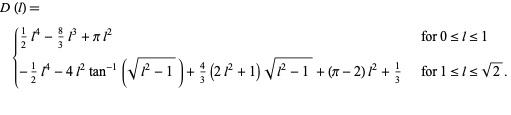 |
(5) |
From this, the mean distance 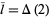 can be computed, as can the variance of lengths,
can be computed, as can the variance of lengths,
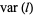 |
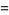 |
![1/(225)[69-4sqrt(2)-10(2+sqrt(2))sinh^(-1)1-25(sinh^(-1)1)^2]](http://mathworld.wolfram.com/images/equations/SquareLinePicking/Inline17.gif) |
(6) |
 |
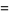 |
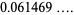 |
(7) |
The statistical median is given by the root of the quartic equation
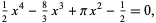 |
(8) |
which is approximately 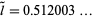 .
.
The 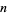 th raw moment is given for
th raw moment is given for 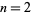 , 4, 6, ... as 1/3, 17/90, 29/210, 187/1575, 239/207, ... (OEIS A103304 and A103305).
, 4, 6, ... as 1/3, 17/90, 29/210, 187/1575, 239/207, ... (OEIS A103304 and A103305).
If, instead of picking two points from the interior of a square, two points are chosen at random on different sides of the unit square, the average distance between two points picked in this manner is
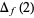 |
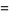 |
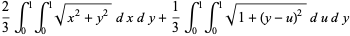 |
(9) |
 |
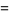 |
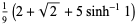 |
(10) |
 |
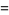 |
![1/9[2+sqrt(2)+5ln(1+sqrt(2))]](http://mathworld.wolfram.com/images/equations/SquareLinePicking/Inline32.gif) |
(11) |
 |
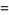 |
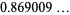 |
(12) |
(OEIS A091506; Borwein and Bailey 2003, p. 25; Borwein et al. 2004, p. 66).
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006b.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Sloane, N. J. A. Sequences A091505, A091506, A103304, and A103305 in "The On-Line Encyclopedia of Integer Sequences."
Trott, M. "The Mathematica Guidebooks Additional Material: Average Distance Distribution." http://www.mathematicaguidebooks.org/additions.shtml#S_1_14.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|