المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Gieseking,s Constant |
 761
 02:09 صباحاً
date: 25-2-2020 |
Author : Finch, S. R. 
Book or Source : Mathematical Constants. Cambridge, England: Cambridge University Press 
Page and Part : ...|
Read More
Date: 30-5-2020
681
Date: 4-11-2019
595
Date: 11-3-2020
571
|
Gieseking's constant is defined by
 |
 |
 |
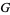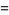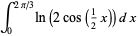(1) |
 |
 |
 |
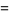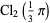(2) |
 |
 |
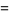![(3sqrt(3))/4[1-sum_(k=0)^(infty)1/((3k+2)^2)+sum_(k=1)^(infty)1/((3k+1)^2)]](http://mathworld.wolfram.com/images/equations/GiesekingsConstant/Inline9.gif) |
(3) |
 |
 |
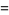![-1/(36)i[pi^2-36Li_2(-(-1)^(2/3))]](http://mathworld.wolfram.com/images/equations/GiesekingsConstant/Inline12.gif) |
(4) |
 |
 |
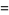![1/2i[Li_2((-1)^(2/3))-Li_2((-1)^(1/3))]](http://mathworld.wolfram.com/images/equations/GiesekingsConstant/Inline15.gif) |
(5) |
 |
 |
 |
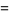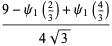(6) |
 |
 |
 |
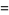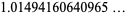(7) |
(OEIS A143298), where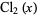 
is Clausen's integral, 
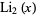is a dilogarithm, and 
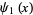is a trigamma function.
REFERENCES:
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 232-233, 2003.
Sloane, N. J. A. Sequence A143298 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
