Heisenberg Uncertainty

The Heisenberg uncertainty principle, also known as the indeterminancy principle worldwide, states Δp_xΔx ≥ h/4π, where Δx is the uncertainty in the x-position measurement, Δp_x is the uncertainty in the x-momentum measurement, and h is Planck’s constant. As some people say, the uncertainty principle places a limit on the accuracy of knowing a particle’s position. What do you think? Some people claim also that the Heisenberg uncertainty principle is just an example of a more general uncertainty relationship for all waves, that the position can be determined only at the expense of our knowledge of its wavelength. Is this statement true?

We also know that Niels Bohr, in his discussions with Albert Einstein over several decades on whether quantum mechanics is a complete description of nature, would often invoke the uncertainty principle to defend his point of view, known as the Copenhagen interpretation of QM. Bohr argued that if you pin down the particle’s position more precisely for the famous double-slit experiment by observing with photons, their interaction with the particle disturbs its momentum by giving it a random momentum kick. That is, without looking, the particle exhibits an interference pattern on a distant screen behind the two slits. However, if you look to see which way the particle goes through the slits, the measurement disturbs the system and there’s no interference pattern on the distant screen. You just see a classical two-hump distribution. What do you think about Bohr’s argument?

Answer

The uncertainty principle places no limit to the accuracy of measuring the particle’s position. The uncertainty principle Δp_xΔx ≥ h/4π forbids the simultaneous measurement of both position and momentum in the same direction to arbitrary accuracy, not an individual measurement. Of course, practical design limitations exist that probably limit the measurement, but conceptually there is no limit. The same argument applies separately to the momentum.

An application of the Heisenberg uncertainty principle to the hydrogen atom is an insightful example. The hydrogen atom is usually solved in spherical polar coordinates instead of Cartesian coordinates. In spherical polar coordinates, the uncertainty relations are a bit more complicated and the consequences can be somewhat bizarre. For example, since the hydrogen wave function for the electron about the z-axis that is, in the φ direction is known precisely for the 1s atomic state, and hence the angular momentum has no uncertainty, the uncertainty in φ is maximum. Therefore, in the φ direction, one finds an equal probability at all angles, producing the smeared-out probability distribution in φ.

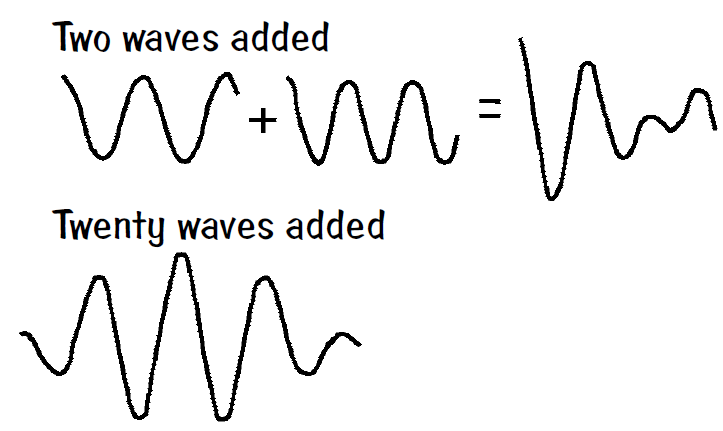
Many other uses for the uncertainty relation exist because it lies at the very heart of quantum mechanics. However, one can see that any description of a phenomenon using waves of any kind will require an uncertainty relation. Engineers are familiar with the fact that about a one-MHz bandwidth is required to reproduce a one microsecond pulse: ΔfΔt ~ 1, for example. Suppose there is a single-frequency wave defined by y = y₁ sin k₁x. This wave extends from – ∞ to + ∞, and the question “where is the wave located?” has no answer. By adding together many single-frequency waves of different frequencies with properly chosen amplitudes and phrases, we can build up a lump in a narrow region of space of approximate length Δx. The range of wavelengths Δλ needed can be represented by the corresponding range of wavenumbers Δk. The approximate mathematical relationship Δ x Δk ~ 1 can be established by considering several examples, as seen in the Krane reference below.

Bohr’s famous measurement disturbance argument is faulty. For half a century physicists have regurgitated this argument of how the uncertainty principle acts to defend quantum theory. In experiments that first refuted Bohr’s argument, a beam of cold rubidium atoms is split to travel along two different paths; call them A and B. The beams still overlap and combine at the end of their journeys to create an interference pattern. Now the researchers looked to see which path the atoms followed by tweaking those on path B into a higher energy state by a pulse of microwaves. These atoms in

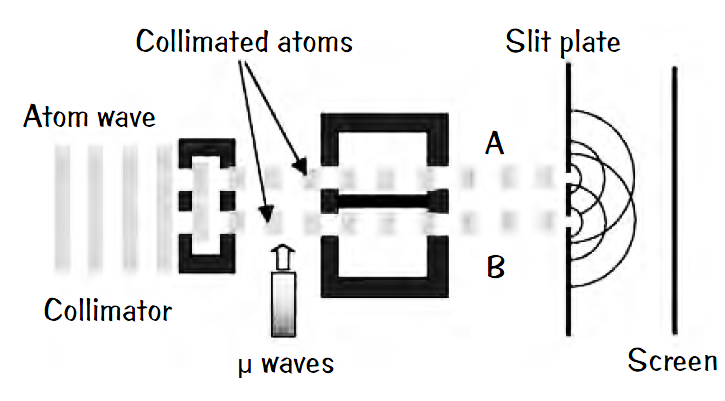
their internal states kept a record of which path they had taken. The microwave pulse absorbed by an atom is insignificant by a factor of about 10,000 and can cause little change to the atom’s momentum, not enough to smear the interference pattern.

Yes, QM worked still. With the microwaves off, interference fringes appear. Turn them on so you can tell which path was taken, and the interference pattern vanishes. The uncertainty principle is correct still, but the argument that “measurement disturbs the system” to explain the double slit experiment is wrong.

So what may be the deeper mechanism at work in the double slit experiment, for example? Perhaps quantum entanglement, in which every particle is linked to every other particle it has interacted with. Two-particle wave functions are linked in a six-dimensional configuration space with no one-to-one correspondence to physical 3-D space, so the entanglement of N particles will be described by a wave function in 3N-dimensional configuration space with no one-to-one correspondence to 3-D physical space. And now the mathematics becomes messier!