
Hair-Raiser Function
 المؤلف:
Franklin Potter and Christopher Jargodzki
المؤلف:
Franklin Potter and Christopher Jargodzki
 المصدر:
Mad about Modern Physics
المصدر:
Mad about Modern Physics
 الجزء والصفحة:
p 123
الجزء والصفحة:
p 123
 24-11-2016
24-11-2016
 1371
1371
Hair-Raiser Function
One of us (F. P.) first heard about the hair-raiser function (HRF) from physicist Richard Feynman. We introduce this function here as a curiosity to stimulate the mind. And if one pulls a hair on top of the head upright, this function is probably a good representation of its fast vertical increase with horizontal distance.
Most mathematical functions are easy to define, and so are their inverses. Physicists utilize a tremendous variety of mathematical functions, the two most common being the power of a quantity and the exponential of a quantity. Physicists also use mathematical operations that may not seem to qualify as a function, such as the Dirac delta function δ(r – r0). Powers are prevalent in fundamental laws dictated by geometrical symmetries such as the universal law of gravitation and the Coulomb law, both having potentials proportional to 1/r and forces proportional to 1/r2 for ideal point sources. The exponential function increases more rapidly than practically any other known function and is used whenever the change in a quantity is proportional to the quantity itself, such as in growths and decays.
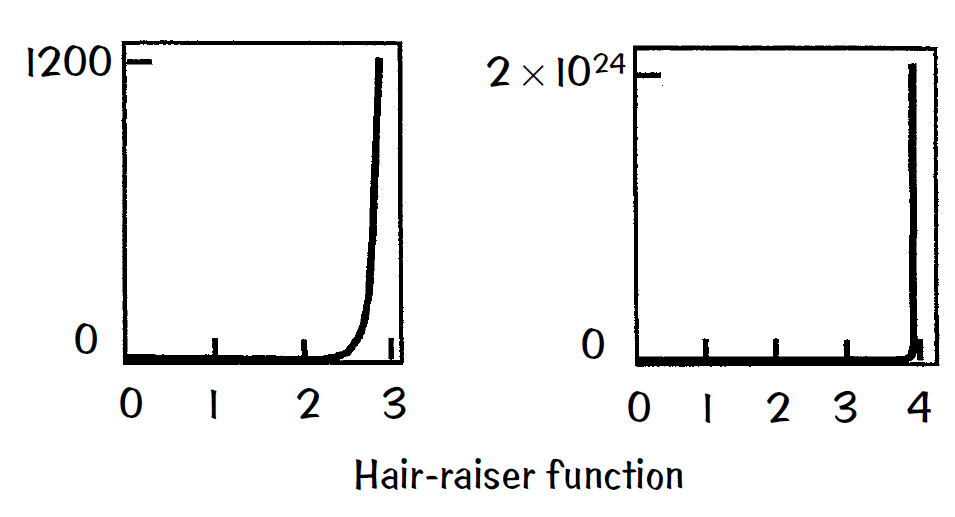
The hair-raiser function HRF(x) can be defined by example on how it maps integers to integers. The HRF(1) is 1. The HRF(2) = 22. The HRF(3) = (33)3, and so on. Notice the grouping with parentheses. One needs a calculator for most of the higher-integer HRFs. Certainly the HRF is a one-to-one mapping.
How does one calculate the HRF of a non-integer? Of a complex number? How does one determine the inverse of the HRF? That is, given a number such as 42, how does one determine what number is mapped by the HRF into 42? And finally, of what potential use is the hair-raiser function?
Answer
For the HRF of a non-integer, one needs to write down a few more examples of the given integer description. Then take the logarithm of each example to discover that they all can be expressed as log N = nn–1 log n. By taking the exponential of both sides with the proper grouping, the final expression becomes N = (n)^(nn–1)—that is, n to the power (nn–1). With HRF(x) = (x)^(xx–1), the HRF of non-integer values for x becomes an easy calculation with the appropriate calculator, one capable of many decimal places. What is the limit as n approaches zero? Complex numbers can be used, as well as irrationals such as π.
A plot of the HRF using integers shows a remarkably steep rise for even small integers; hence its name! You might want to compare its rise to an exponential function. And if all you desire is an approximate value for the inverse or for the HRF of a non-integer, the plot provides a visual image and a means to satisfy your curiosity.
However, as far as we know, the inverse HRF is awkward, and no easy calculation algorithm is known. We don’t even know whether the inverse can be expressed as the limit of a series! One can determine the inverse by successive approximation to any number of decimal places with the appropriate calculator.
Of what use is the hair-raiser function? The question reminds us of two classic quotes from Michael Faraday when he was attempting to explain a discovery to the visiting prime minister. He was asked: “But, after all, what use is it?” To which Faraday replied, “Why, sir, there is the probability that you will soon be able to tax it.” And when the prime minister asked of a new discovery, “What good is it?,” Faraday replied, “What good is a newborn baby?”
 الاكثر قراءة في طرائف الفيزياء
الاكثر قراءة في طرائف الفيزياء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


