


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-9-2021
Date: 22-12-2021
Date: 23-8-2021
|
A problem in game theory first discussed by A. Tucker. Suppose each of two prisoners 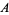 and
and 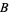 , who are not allowed to communicate with each other, is offered to be set free if he implicates the other. If neither implicates the other, both will receive the usual sentence. However, if the prisoners implicate each other, then both are presumed guilty and granted harsh sentences.
, who are not allowed to communicate with each other, is offered to be set free if he implicates the other. If neither implicates the other, both will receive the usual sentence. However, if the prisoners implicate each other, then both are presumed guilty and granted harsh sentences.
A dilemma arises in deciding the best course of action in the absence of knowledge of the other prisoner's decision. Each prisoner's best strategy would appear to be to turn the other in (since if 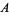 makes the worst-case assumption that
makes the worst-case assumption that 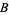 will turn him in, then
will turn him in, then 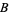 will walk free and
will walk free and 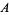 will be stuck in jail if he remains silent). However, if the prisoners turn each other in, they obtain the worst possible outcome for both.
will be stuck in jail if he remains silent). However, if the prisoners turn each other in, they obtain the worst possible outcome for both.
Mosteller (1987) describes a different problem he terms "the prisoner's dilemma." In this problem, three prisoners 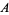 ,
, 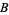 , and
, and 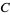 with apparently equally good records have applied for parole, and the parole board has decided to release two, but not all three. A warder knows which two are to be released, and one of the prisoners (
with apparently equally good records have applied for parole, and the parole board has decided to release two, but not all three. A warder knows which two are to be released, and one of the prisoners (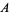 ) asks the warder for the name of the one prisoner other than himself who is to be released. While his chances of being released before asking are 2/3, he thinks his chances after asking and being told "
) asks the warder for the name of the one prisoner other than himself who is to be released. While his chances of being released before asking are 2/3, he thinks his chances after asking and being told "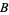 will be released" are reduced to 1/2, since now either
will be released" are reduced to 1/2, since now either 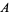 and
and 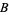 or
or 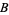 and
and 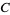 are to be released. However, he is mistaken since his chances remain 2/3.
are to be released. However, he is mistaken since his chances remain 2/3.
The Season 1 episode "Dirty Bomb" (2005) of the television crime drama NUMB3RS mentions the Prisoner's dilemma.
REFERENCES:
Axelrod, R. The Evolution of Cooperation. New York: BasicBooks, 1985.
Erickson, G. W. and Fossa, J. A. Dictionary of Paradox. Lanham, MD: University Press of America, pp. 164-165, 1998.
Goetz, P. "Phil Goetz's Complexity Dictionary." http://www.cs.buffalo.edu/~goetz/dict.html
Mosteller, F. "The Prisoner's Dilemma." Problem 13 in Fifty Challenging Problems in Probability with Solutions. New York: Dover, pp. 4 and 14-15, 1987.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|