


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-6-2021
Date: 17-6-2021
Date: 6-7-2017
|
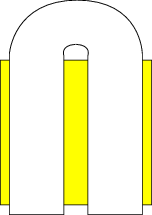
The Smale horseshoe map consists of a sequence of operations on the unit square. First, stretch in the 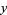 direction by more than a factor of two, then compress in the
direction by more than a factor of two, then compress in the  direction by more than a factor of two. Finally, fold the resulting rectangle and fit it back onto the square, overlapping at the top and bottom, and not quite reaching the ends to the left and right (and with a gap in the middle), as illustrated in the diagram above. The shape of the stretched and folded map gives the horseshoe map its name. Note that it is vital to the construction process for the map to overlap and leave the middle and vertical edges of the initial unit square uncovered.
direction by more than a factor of two. Finally, fold the resulting rectangle and fit it back onto the square, overlapping at the top and bottom, and not quite reaching the ends to the left and right (and with a gap in the middle), as illustrated in the diagram above. The shape of the stretched and folded map gives the horseshoe map its name. Note that it is vital to the construction process for the map to overlap and leave the middle and vertical edges of the initial unit square uncovered.
Repeating this generates the horseshoe attractor. If one looks at a cross section of the final structure, it is seen to correspond to a Cantor set.
The Smale horseshoe map is the set of basic topological operations for constructing an attractor consist of stretching (which gives sensitivity to initial conditions) and folding (which gives the attraction). Since trajectories in phase space cannot cross, the repeated stretching and folding operations result in an object of great topological complexity. The Smale horseshoe map is the same topological structure as the homoclinic tangle.
REFERENCES:
Gleick, J. Chaos: Making a New Science. New York: Penguin, pp. 50-51, 1988.
Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, p. 77, 1990.
Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, 1989.a



|
|
|
|
كل ما تود معرفته عن أهم فيتامين لسلامة الدماغ والأعصاب
|
|
|
|
|
|
|
ماذا سيحصل للأرض إذا تغير شكل نواتها؟
|
|
|
|
|
|
|
بالتعاون مع العتبة العباسية مهرجان الشهادة الرابع عشر يشهد انعقاد مؤتمر العشائر في واسط
|
|
|