المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Class Equation |
 544
 04:48 مساءً
date: 17-8-2020 |
Author : Cox, D. A 
Book or Source : Primes of the Form x2+ny2: Fermat, Class Field Theory and Complex Multiplication. New York: Wiley, 1997. 
Page and Part : ...|
Read More
Date: 22-11-2019
764
Date: 6-1-2021
940
Date: 25-10-2020
816
|
Let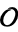 
be an order of an imaginary quadratic field. The class equation of 
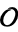is the equation 
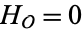, where 
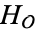is the extension field minimal polynomial of 
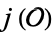over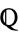 
, with 
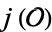the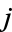 
-invariant of 
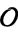. (If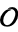 
has generator 
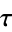, then 
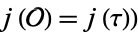. The degree of 
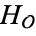is equal to the class number of the field of fractions 
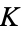of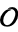 
.
The polynomial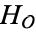 
is also called the class equation of 
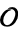(e.g., Cox 1997, p. 293).
It is also true that
![H_O(X)=product[X-j(a)],](https://mathworld.wolfram.com/images/equations/ClassEquation/NumberedEquation1.gif) |
where the product is over representatives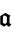 
of each ideal class of 
.
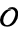If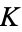 
has discriminant 
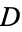, then the notation 
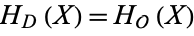is used. If 
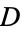is not divisible by 3, the constant term of 
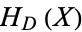is a perfect cube. The table below lists the first few class equations as well as the corresponding values of 
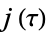, with 
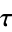being generators of ideals in each ideal class of 
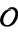. In each case, the constant term is written out as a cube times a cubefree part.
 |
 |
 |
 |
 |
 |
 |
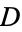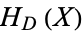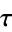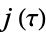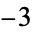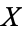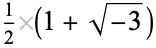0 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
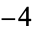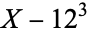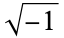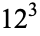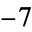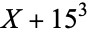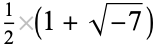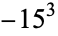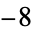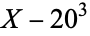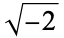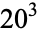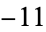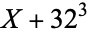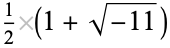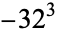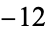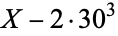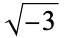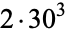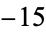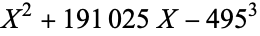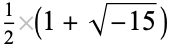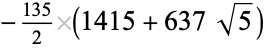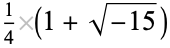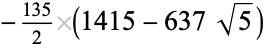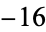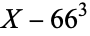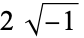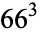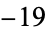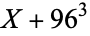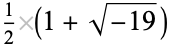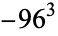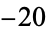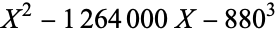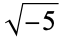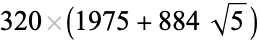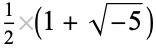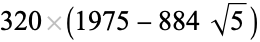REFERENCES:
Cox, D. A. Primes of the Form x2+ny2: Fermat, Class Field Theory and Complex Multiplication. New York: Wiley, 1997.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
