


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2023-02-11
التاريخ: 27-4-2016
التاريخ: 26-4-2016
التاريخ: 24-7-2016
|
تحويلات لورنس واستخدام المصفوفات
ينبغي علينا قبل كل شيء مناقشة التحويل التعامدي في الفضاء ذي الابعاد الثلاثة ثم نطبق نتائج هذا النوع من التحويل ليشمل الفضاء ذا الابعاد الاربعة وذلك بان يضاف الاحداثي الرابع x4.
يكون التحويل خطيا لمجموعة من الاحداثيات اذا امكن التعبير عنها بالإحداثيات الاصلية على النحو التالي :
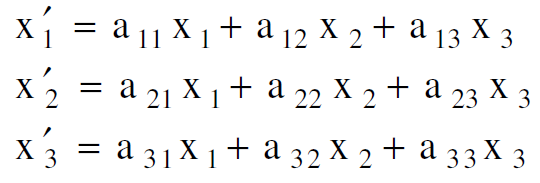
او :
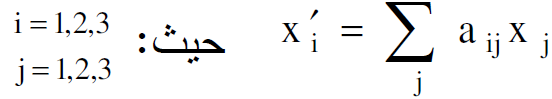 (1.1)
(1.1)
وهذا التحويل يسمى بالتحويل الخطي وان aij تمثل مجموعة من المعاملات التي توصف هذا التحويل. ويصبح هذا التحويل تعامديا اذا بقي مقدار المتجه x2i Σ دون تغيير. فاذا فرض ان المعادلة الاخيرة تمثل تحويلا تعامديا يكون :
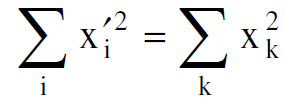 (1.2)
(1.2)
وبما أن :
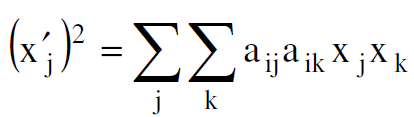
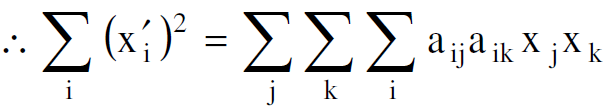 (1.3)
(1.3)
وتتساوى العلاقتان (1.2) و (1.3) عندما يكون :
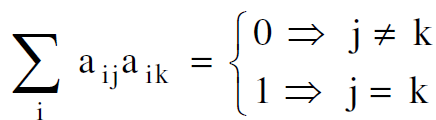
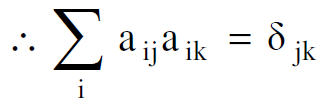 (1.4)
(1.4)
ولجعل التحويل انف الذكر تحويلا تعامديا ينبغي ان تتحقق العلاقة (1.4).
إن التحويل الذي تعطيه العلاقة (1.1) يمكن كتابته على النحو الآتي :
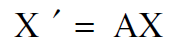 (1.5)
(1.5)
حيث ان Xʹ تمثل متجه الموضع المحول مع مركباته (3ʹxʹ1, xʹ2, x) وان X متجه الموضع الاصلي مع مركباته (x1, x2, x3) وان A تمثل مصفوفة التحويل بعناصرها aij ونكتب :
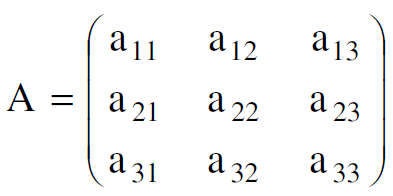
واذا مثلنا المتجهين X, Xʹ كمصفوفتين بمعمود واحد يمكننا ان نكتب :
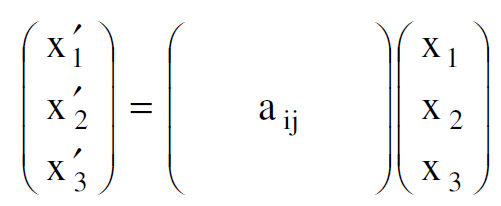 (1.6)
(1.6)
و aij هي مصفوفة الدوران الخاصة بهذا التحويل. ان طريقة التحويل باستخدام المصفوفات يمكن تطبيقها بالنسبة للقضاء ذي الابعاد الاربعة.
لنفرض ان ℓ طول متجه في هذا القضاء مربعه 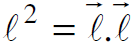
يمكن ان يكتب :
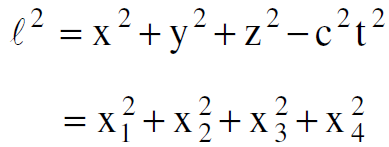
والخاصية الاساسية لتحويلات لورنس ان ℓ يترك دون تغيير تحت تحويلات لورنس اي ان :
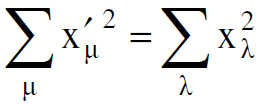
من الممكن الان كتابة معادلات لورنس على النحو الآتي :
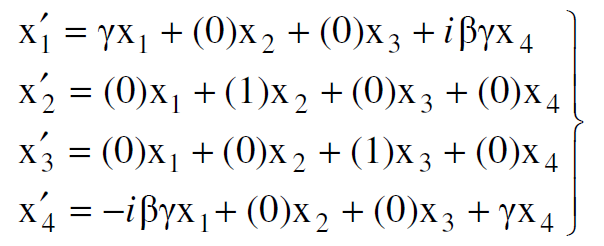 (1.7)
(1.7)
حيث ان  وان
وان 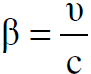 , v السرعة النسبية بين محوري الاسناد sʹ, s.
, v السرعة النسبية بين محوري الاسناد sʹ, s.
ويمكن التعبير عن تحويلات لورنس بصيغة المصفوفة بشكل :
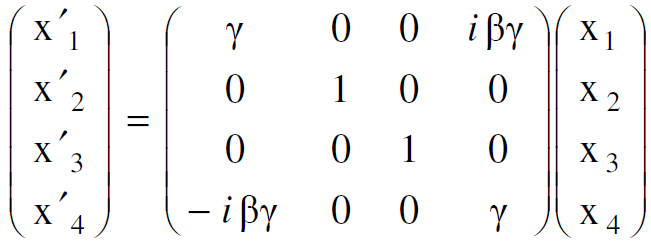 (1.8)
(1.8)
ان مصفوفة التحويل المبينة بالعلاقة (1.8) هي تحويل تعامدي اي ان عناصرها تخضع للعلاقة (1.4). وهي سهلة التعامل بين محوري اسناد بينهما حركة نسبية باتجاه المحور x. وهكذا نجد أن x و t يتحولان الى ʹx وtʹ بينما الاتجاهان y و z لا يتأثران بهذا التحويل.
ان تحويل لورنس الممثل بالمعادلة (1.7) يمكن ان يفسر كدوران في المستوى x1x4. وفي هذه الحالة فان زاوية الدوران Ψ يمكن تحديدها من معادلتي التحويل الاتيتين :
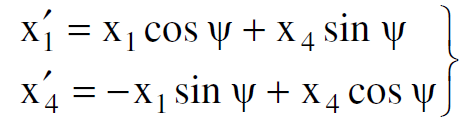 (1.9)
(1.9)
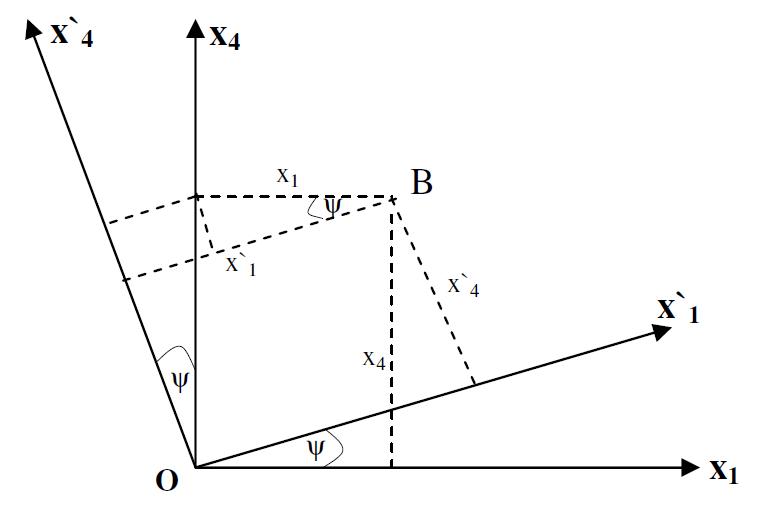
الشكل (1.1) : تحويل في اربعة ابعاد. زاوية الدوران .. هي زاوية خيالية.
وبمقارنة العلاقة (1.9) بالعلاقة (1.7) يتضح لدينا ان :
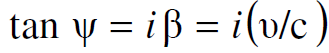 (1.10)
(1.10)
وهكذا نستنتج ان زاوية الدوران ليست زاوية حقيقية، رياضيا نقول ان تحويل لورنس يعتبر دورانا في قضاء تعامدي ذي أبعاد اربعة، الا انه دور أن خلال زاوية خيالية. من العلاقة (1.10) ومعادلات التحويل نستنتج أن :
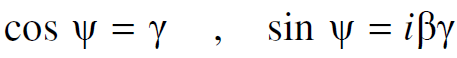
اذن يمكننا كتابة مصفوفة التحويل على النحو التالي :
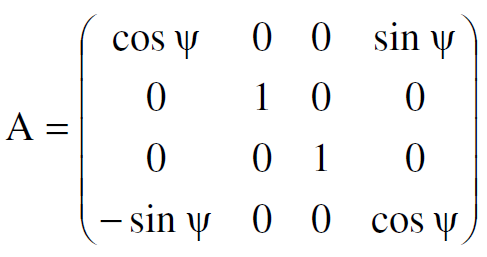 (1.11)
(1.11)
من أهم فوائد المصفوفات في النسبية معالجة التراكيب المتعلقة بتحويلات لورنس اذ تسهل العمليات بواسطة ضرب المصفوفات.
نستنتج مما تقدم ان المتجه الرباعي بصورة عامة يمكن تعريفه بانه مجموعة لأربع كميات، واذا كان المتجه هو 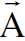 فالكميات الاربع هي (Aμ)، حيث μ =1,2,3,4، وهذه الكميات الاربع تتحول بالطريقة نفسها التي تتحول فيها الاحداثيات .. بالنسبة لتحويلات لورنس. وهكذا تكتب معادلة التحويل الاتية :
فالكميات الاربع هي (Aμ)، حيث μ =1,2,3,4، وهذه الكميات الاربع تتحول بالطريقة نفسها التي تتحول فيها الاحداثيات .. بالنسبة لتحويلات لورنس. وهكذا تكتب معادلة التحويل الاتية :
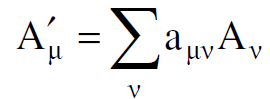 (1.12)
(1.12)
حيث أن :
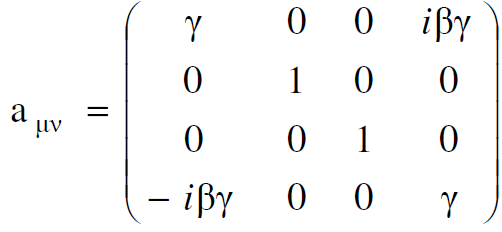 (1.13)
(1.13)



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
الأمانة العامة للعتبة الكاظمية المقدسة تستذكر فاجعة البقيع
|
|
|