
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Conservation of angular momentum
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 18
2024-02-29
1561
Now we shall go on to consider what happens when there is a large number of particles, when an object is made of many pieces with many forces acting between them and on them from the outside. Of course, we already know that, about any given fixed axis, the torque on the ith particle (which is the force on the ith particle times the lever arm of that force) is equal to the rate of change of the angular momentum of that particle, and that the angular momentum of the ith particle is its momentum times its momentum lever arm. Now suppose we add the torques τi for all the particles and call it the total torque τ. Then this will be the rate of change of the sum of the angular momenta of all the particles Li, and that defines a new quantity which we call the total angular momentum L. Just as the total momentum of an object is the sum of the momenta of all the parts, so the angular momentum is the sum of the angular momenta of all the parts. Then the rate of change of the total L is the total torque:

Now it might seem that the total torque is a complicated thing. There are all those internal forces and all the outside forces to be considered. But, if we take Newton’s law of action and reaction to say, not simply that the action and reaction are equal, but also that they are directed exactly oppositely along the same line (Newton may or may not actually have said this, but he tacitly assumed it), then the two torques on the reacting objects, due to their mutual interaction, will be equal and opposite because the lever arms for any axis are equal. Therefore, the internal torques balance out pair by pair, and so we have the remarkable theorem that the rate of change of the total angular momentum about any axis is equal to the external torque about that axis!
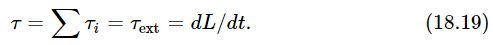
Thus, we have a very powerful theorem concerning the motion of large collections of particles, which permits us to study the overall motion without having to look at the detailed machinery inside. This theorem is true for any collection of objects, whether they form a rigid body or not.
One extremely important case of the above theorem is the law of conservation of angular momentum: if no external torques act upon a system of particles, the angular momentum remains constant.
A special case of great importance is that of a rigid body, that is, an object of a definite shape that is just turning around. Consider an object that is fixed in its geometrical dimensions, and which is rotating about a fixed axis. Various parts of the object bear the same relationship to one another at all times. Now let us try to find the total angular momentum of this object. If the mass of one of its particles is mi, and its position or location is at (xi,yi), then the problem is to find the angular momentum of that particle, because the total angular momentum is the sum of the angular momenta of all such particles in the body. For an object going around in a circle, the angular momentum, of course, is the mass times the velocity times the distance from the axis, and the velocity is equal to the angular velocity times the distance from the axis:
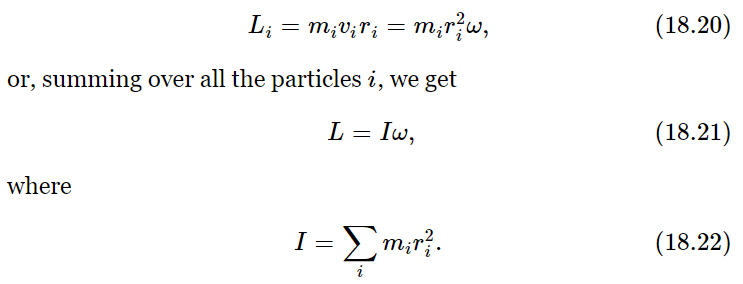
This is the analog of the law that the momentum is mass times velocity. Velocity is replaced by angular velocity, and we see that the mass is replaced by a new thing which we call the moment of inertia I, which is analogous to the mass. Equations (18.21) and (18.22) say that a body has inertia for turning which depends, not just on the masses, but on how far away they are from the axis. So, if we have two objects of the same mass, when we put the masses farther away from the axis, the inertia for turning will be higher. This is easily demonstrated by the apparatus shown in Fig. 18–4, where a weight M is kept from falling very fast because it has to turn the large weighted rod. At first, the masses m are close to the axis, and M speeds up at a certain rate. But when we change the moment of inertia by putting the two masses m much farther away from the axis, then we see that M accelerates much less rapidly than it did before, because the body has much more inertia against turning. The moment of inertia is the inertia against turning, and is the sum of the contributions of all the masses, times their distances squared, from the axis.

Fig. 18–4. The “inertia for turning” depends upon the lever arm of the masses.
There is one important difference between mass and moment of inertia which is very dramatic. The mass of an object never changes, but its moment of inertia can be changed. If we stand on a frictionless rotatable stand with our arms outstretched, and hold some weights in our hands as we rotate slowly, we may change our moment of inertia by drawing our arms in, but our mass does not change. When we do this, all kinds of wonderful things happen, because of the law of the conservation of angular momentum: If the external torque is zero, then the angular momentum, the moment of inertia times omega, remains constant. Initially, we were rotating with a large moment of inertia I1 at a low angular velocity ω1, and the angular momentum was I1ω1. Then we changed our moment of inertia by pulling our arms in, say to a smaller value I2. Then the product Iω, which has to stay the same because the total angular momentum has to stay the same, was I2ω2. So I1ω1=I2ω2. That is, if we reduce the moment of inertia, we have to increase the angular velocity.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















