المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر
أضيف حديثاً
مـقايـيس الجـودة والرضـا لتـقييـم تـجربـة إعـادة الهـيكلـة
2024-11-06
مقاييس الإنتاجية لتـقييـم تـجربـة إعـادة الهـيكلـة
2024-11-06
تقييم تجربة إعادة الهيكلة (مقاييس الالتزام بالخطة)
2024-11-06
السـيطـرة عـلـى مـقاومـة التـغيـير فـي المنظمـات
2024-11-06
إعـداد خـطـة إعـادة الهـيكـلـة 2
2024-11-06
أزواج النبي "ص" يشاركن في الصراع على الخلافة
2024-11-06

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
الشبكات الاجتماعية
2023-04-13
الشاب والصراعات النفسية
2023-08-22
مفهوم الجريمة
29-3-2016
Implies
12-2-2022
Orthography
2024-04-26
بطلان الصوم في سفر القصر وسقوط نوافل النهار.
15-1-2016

Lubbock,s Formula  
  
488   05:20 مساءً   date: 9-12-2021
Author : Lubbock, J. W
Book or Source : Cambridge Philos. Trans. 3
Page and Part : ...


Read More
Descartes, Sign Rule
Date: 10-12-2021 498
Maehly,s Procedure
Date: 12-12-2021 673
T-Integration
Date: 8-12-2021 336

Lubbock,s Formula

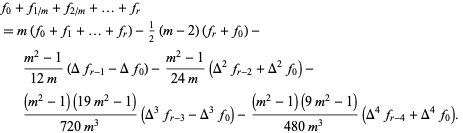f_0+f_(1/m)+f_(2/m)+...+f_r =m(f_0+f_1+...+f_r)-1/2(m-2)(f_r+f_0)-(m^2-1)/(12m)(Deltaf_(r-1)-Deltaf_0)-(m^2-1)/(24m)(Delta^2f_(r-2)+Delta^2f_0)-((m^2-1)(19m^2-1))/(720m^3)(Delta^3f_(r-3)-Delta^3f_0)-((m^2-1)(9m^2-1))/(480m^3)(Delta^4f_(r-4)+Delta^4f_0).

REFERENCES:

Lubbock, J. W. Cambridge Philos. Trans. 3, 323, 1829.

Whittaker, E. T. and Robinson, G. "Lubbock's Formula of Summation." §74 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 149-150, 1967.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
التاريخ / 2024-11-04

الأخبار العلمية
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
التاريخ / 2024-11-04

الساحة الاسلامية
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
التاريخ / 2024-11-06