


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-12-2021
Date: 14-12-2021
Date: 5-12-2021
|
T-integration, which stands for "tunable numerical integration," is a fast, accurate, and numerically stable numerical integration formula given by
![X_n=X_(n-1)+TG[P((dX)/(dt))_n+(1-P)((dX)/(dt))_(n-1)],](https://mathworld.wolfram.com/images/equations/T-Integration/NumberedEquation1.gif) |
where 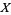 is the integral,
is the integral, 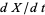 is the integrand,
is the integrand, 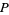 and
and 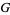 are "phase" and "gain" tuning parameters,
are "phase" and "gain" tuning parameters, 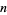 refers to the number of the iteration being evaluated, and
refers to the number of the iteration being evaluated, and 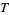 is the integration step size.
is the integration step size.
The method was developed during the Apollo era to figure out how to simulate the digitally controlled Apollo command module during rendezvous and lunar landing operations. It was needed because none of the classical numerical integrators worked when trying to simulate the digital flight control systems maneuvering a space craft to a lunar landing.
For 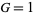 , varying
, varying 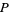 from 0 to 2 gives many classical first-order integrators:
from 0 to 2 gives many classical first-order integrators:
1. 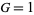 and
and 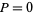 : Euler integrator,
: Euler integrator,
2. 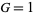 and
and 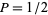 : trapezoidal rule,
: trapezoidal rule,
3. 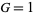 and
and 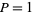 : Rectangular rule,
: Rectangular rule,
4. 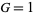 and
and 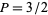 : Adams' method.
: Adams' method.
REFERENCES:
Fowler, M. "A New Numerical Method for Simulation." Simulation 6, 90-92, Feb. 1976.
Smith, J. M. "Recent Developments in Numerical Integration." J. Dynam. Sys., Measurement and Control 96, Ser. G-1, No. 1, 61-70, Mar. 1974.
Smith, J. M. "Zero-Order T-Integration and Its Relation to the Mean Value Theorem." In Proceedings of the Sixth Annual Pittsburgh Modeling and Simulation Conference, Part 1, April 24-25, 1975.
Smith, J. M. "Modern Numerical Integration Methods." In Mathematical Modeling and Digital Simulation, 2nd ed. New York: John Wiley, 1988.
Smith, J. M. "Fast T-Integration." J. Mech. Eng. Sys. 1, 27-31, Jul./Aug. 1990.
Smith, J. M. "Jon Michael Smith on T-Integration: Trade Secrets in Numerical Analysis." http://members.aol.com/jsmith46ws/ni1.htm.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|