


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-12-2021
Date: 2-12-2021
Date: 10-12-2021
|
A Gaussian quadrature-like formula for numerical estimation of integrals. It requires 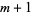 points and fits all polynomials to degree
points and fits all polynomials to degree 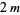 , so it effectively fits exactly all polynomials of degree
, so it effectively fits exactly all polynomials of degree 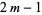 . It uses a weighting function
. It uses a weighting function 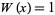 in which the endpoint
in which the endpoint 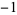 in the interval
in the interval ![[-1,1]](https://mathworld.wolfram.com/images/equations/RadauQuadrature/Inline6.gif) is included in a total of
is included in a total of 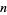 abscissas, giving
abscissas, giving 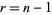 free abscissas. The general formula is
free abscissas. The general formula is
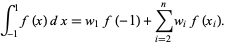 |
(1) |
The free abscissas 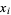 for
for 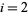 , ...,
, ..., 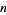 are the roots of the polynomial
are the roots of the polynomial
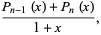 |
(2) |
where 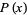 is a Legendre polynomial. The weights of the free abscissas are
is a Legendre polynomial. The weights of the free abscissas are
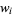 |
 |
![(1-x_i)/(n^2[P_(n-1)(x_i)]^2)](https://mathworld.wolfram.com/images/equations/RadauQuadrature/Inline15.gif) |
(3) |
 |
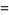 |
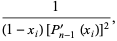 |
(4) |
and of the endpoint
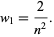 |
(5) |
The error term is given by
![E=(2^(2n-1)n[(n-1)!]^4)/([(2n-1)!]^3)f^((2n-1))(xi),](https://mathworld.wolfram.com/images/equations/RadauQuadrature/NumberedEquation4.gif) |
(6) |
for 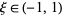 .
.
 |
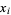 |
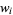 |
| 2 | 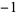 |
0.5 |
| 0.333333 | 1.5 | |
| 3 | 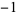 |
0.222222 |
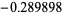 |
1.02497 | |
| 0.689898 | 0.752806 | |
| 4 | 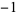 |
0.125 |
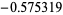 |
0.657689 | |
| 0.181066 | 0.776387 | |
| 0.822824 | 0.440924 | |
| 5 | 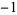 |
0.08 |
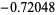 |
0.446208 | |
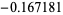 |
0.623653 | |
| 0.446314 | 0.562712 | |
| 0.885792 | 0.287427 |
The abscissas and weights can be computed analytically for small 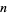 .
.
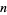 |
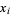 |
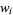 |
| 2 | 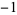 |
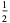 |
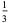 |
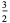 |
|
| 3 | 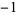 |
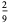 |
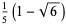 |
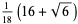 |
|
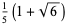 |
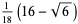 |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 888, 1972.
Chandrasekhar, S. Radiative Transfer. New York: Dover, p. 61, 1960.
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 338-343, 1956.
Ueberhuber, C. W. Numerical Computation 2: Methods, Software, and Analysis. Berlin: Springer-Verlag, p. 105, 1997.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|