المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Shovelton,s Rule |
 582
 07:52 مساءً
date: 8-12-2021 |
Author : King, A. E 
Book or Source : "Approximate Integration. Note on Quadrature Formulae: Their Construction and Application to Actuarial Functions." Trans. Faculty of Actuaries 9, 
Page and Part : ...|
Read More
Date: 2-12-2021
309
Date: 7-12-2021
537
Date: 10-12-2021
616
|
Let the values of a function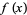 
be tabulated at points 
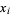equally spaced by 
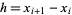, so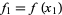 
, 
, ..., 
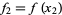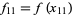. Then Shovelton's rule approximating the integral of 
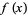is given by the Newton-Cotes-like formula
![int_(x_1)^(x_(11))f(x)dx=5/(126)h[8(f_1+f_(11))+35(f_2+f_4+f_8+f_(10))
+15(f_3+f_5+f_7+f_9)+36f_6].](https://mathworld.wolfram.com/images/equations/ShoveltonsRule/NumberedEquation1.gif) |
REFERENCES:
King, A. E. "Approximate Integration. Note on Quadrature Formulae: Their Construction and Application to ActuHelvetica Functions." Trans. Faculty of Actuaries 9, 218-231, 1923.
Sheppard, W. F. "Some Quadrature-Formulæ." Proc. London Math. Soc. 32, 258-277, 1900.
Whittaker, E. T. and Robinson, G. The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, p. 151, 1967.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
