Rule 50

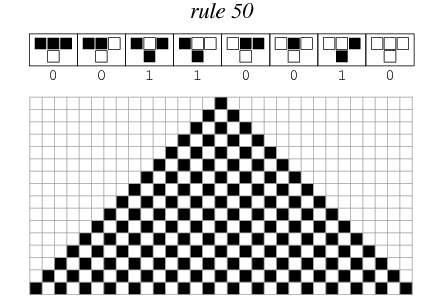
Rule 50 is one of the elementary cellular automaton rules introduced by Stephen Wolfram in 1983 (Wolfram 1983, 2002). It specifies the next color in a cell, depending on its color and its immediate neighbors. Its rule outcomes are encoded in the binary representation 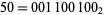. This rule is illustrated above together with the evolution of a single black cell it produces after 15 steps (Wolfram 2002, p. 55).

Note that for initial conditions of a single black cell, rule 50 is equivalent to rules 58, 114, 122, 178, 186, 242, and 250, which are precisely those rules with binary representation 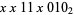. Variants obtained by complementing and mirror reversing and complementing are rules 160, 161, 162, 163, 176, 177, 178, and 179.

Starting with a single black cell, successive generations 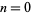, 1, ... are given by interpreting the numbers 1, 5, 21, 85, 341, 1365, 5461, 21845, 87381, 349525, ... (OEIS A002450) in binary, namely 1, 101, 10101, ... (OEIS A071028). The 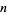th term is given by

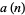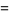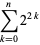			(1)
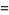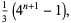			(2)

so computation of the 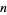th generation is computationally reducible for an initial configuration consisting of a single black cell.  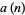has generating function

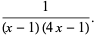(3)

REFERENCES:

Sloane, N. J. A. Sequences A002450/M3914 and A071028 in "The On-Line Encyclopedia of Integer Sequences."

Wolfram, S. "Statistical Mechanics of Cellular Automata." Rev. Mod. Phys. 55, 601-644, 1983.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 55, 90, and 952, 2002.