


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات The arf invariant is a link invariant that always has the value 0 or 1. A knot has Arf invariant 0 if the knot is "pass equivalent" to the unknot and 1 if it is pass equivalent to the trefoil knot.
Arf invariants are implemented in the Wolfram Language as KnotData[knot, "ArfInvariant"].
The numbers of prime knots on 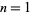 , 2, ... crossings having Arf invariants 0 and 1 are summarized in the table below.
, 2, ... crossings having Arf invariants 0 and 1 are summarized in the table below.
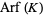 |
OEIS | counts of prime knots with 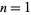 , 2, ... crossings , 2, ... crossings |
| 0 | A131433 | 0, 0, 0, 0, 1, 1, 3, 10, 25, 82, ... |
| 1 | A131434 | 0, 0, 1, 1, 1, 2, 4, 11, 24, 83, ... |
If 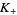 ,
, 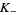 , and
, and 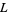 are projections which are identical outside the region of the crossing diagram, and
are projections which are identical outside the region of the crossing diagram, and 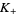 and
and 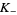 are knots while
are knots while 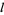 is a 2-component link with a nonintersecting crossing diagram where the two left and right strands belong to the different links, then
is a 2-component link with a nonintersecting crossing diagram where the two left and right strands belong to the different links, then
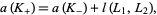 |
(1) |
where 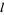 is the linking number of
is the linking number of 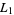 and
and 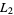 .
.
The Arf invariant can be determined from the Alexander polynomial or Jones polynomial for a knot. For 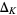 the Alexander polynomial of
the Alexander polynomial of 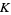 , the Arf invariant is given by
, the Arf invariant is given by
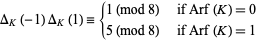 |
(2) |
(Jones 1985). Here, the 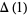 factor takes care of the ambiguity introduced by the fact that the Alexander polynomial is defined only up to multiples of
factor takes care of the ambiguity introduced by the fact that the Alexander polynomial is defined only up to multiples of 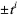 . (Alternately, this indeterminacy is also taken care of by the Conway definition of the polynomial.)
. (Alternately, this indeterminacy is also taken care of by the Conway definition of the polynomial.)
For the Jones polynomial 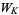 of a knot
of a knot 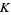 ,
,
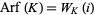 |
(3) |
(Jones 1985), where i is the imaginary number.
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 223-231, 1994.
Jones, V. "A Polynomial Invariant for Knots via von Neumann Algebras." Bull. Amer. Math. Soc. 12, 103-111, 1985.
Sloane, N. J. A. Sequences A131433 and A131434 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|