


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-7-2021
Date: 11-5-2021
Date: 21-6-2017
|
In mathematics, a knot is defined as a closed, non-self-intersecting curve that is embedded in three dimensions and cannot be untangled to produce a simple loop (i.e., the unknot). While in common usage, knots can be tied in string and rope such that one or more strands are left open on either side of the knot, the mathematical theory of knots terms an object of this type a "braid" rather than a knot. To a mathematician, an object is a knot only if its free ends are attached in some way so that the resulting structure consists of a single looped strand.
A knot can be generalized to a link, which is simply a knotted collection of one or more closed strands.
The study of knots and their properties is known as knot theory. Knot theory was given its first impetus when Lord Kelvin proposed a theory that atoms were vortex loops, with different chemical elements consisting of different knotted configurations (Thompson 1867). P. G. Tait then cataloged possible knots by trial and error. Much progress has been made in the intervening years.
Schubert (1949) showed that every knot can be uniquely decomposed (up to the order in which the decomposition is performed) as a knot sum of a class of knots known as prime knots, which cannot themselves be further decomposed (Livingston 1993, p. 5; Adams 1994, pp. 8-9). Knots that can be so decomposed are then known as composite knots. The total number (prime plus composite) of distinct knots (treating mirror images as equivalent) having 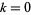 , 1, ... crossings are 1, 0, 0, 1, 1, 2, 5, 8, 25, ... (OEIS A086825).
, 1, ... crossings are 1, 0, 0, 1, 1, 2, 5, 8, 25, ... (OEIS A086825).
Klein proved that knots cannot exist in an even-dimensional space 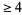 . It has since been shown that a knot cannot exist in any dimension
. It has since been shown that a knot cannot exist in any dimension 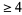 . Two distinct knots cannot have the same knot complement (Gordon and Luecke 1989), but two links can! (Adams 1994, p. 261).
. Two distinct knots cannot have the same knot complement (Gordon and Luecke 1989), but two links can! (Adams 1994, p. 261).
Knots are most commonly cataloged based on the minimum number of crossings present (the so-called link crossing number). Thistlethwaite has used Dowker notation to enumerate the number of prime knots of up to 13 crossings, and alternating knots up to 14 crossings. In this compilation, mirror images are counted as a single knot type. Hoste et al. (1998) subsequently tabulated all prime knots up to 16 crossings. Hoste and Weeks subsequently began compiling a list of 17-crossing prime knots (Hoste et al. 1998).
Another possible representation for knots uses the braid group. A knot with 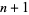 crossings is a member of the braid group
crossings is a member of the braid group 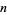 .
.
There is no general algorithm to determine if a tangled curve is a knot or if two given knots are interlocked. Haken (1961) and Hemion (1979) have given algorithms for rigorously determining if two knots are equivalent, but they are too complex to apply even in simple cases (Hoste et al. 1998).
The following tables give the number of distinct prime, alternating, nonalternating, torus, and satellite knots for 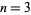 to 16 (Hoste et al. 1998).
to 16 (Hoste et al. 1998).
 |
prime knots | prime alternating knots | prime nonalternating knots | torus knots | satellite knots |
| Sloane | A002863 | A002864 | A051763 | A051764 | A051765 |
| 3 | 1 | 1 | 0 | 1 | 0 |
| 4 | 1 | 1 | 0 | 0 | 0 |
| 5 | 2 | 2 | 0 | 1 | 0 |
| 6 | 3 | 3 | 0 | 0 | 0 |
| 7 | 7 | 7 | 0 | 1 | 0 |
| 8 | 21 | 18 | 3 | 1 | 0 |
| 9 | 49 | 41 | 8 | 1 | 0 |
| 10 | 165 | 123 | 42 | 1 | 0 |
| 11 | 552 | 367 | 185 | 1 | 0 |
| 12 | 2176 | 1288 | 888 | 0 | 0 |
| 13 | 9988 | 4878 | 5110 | 1 | 2 |
| 14 | 46972 | 19536 | 27436 | 1 | 2 |
| 15 | 253293 | 85263 | 168030 | 2 | 6 |
| 16 | 1388705 | 379799 | 1008906 | 1 | 10 |
The numbers of chiral noninvertible 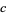 ,
, 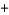 amphichiral noninvertible,
amphichiral noninvertible, 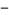 amphichiral noninvertible, chiral invertible
amphichiral noninvertible, chiral invertible 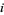 , and fully amphichiral and invertible knots
, and fully amphichiral and invertible knots 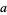 are summarized in the following table for
are summarized in the following table for 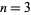 to 16 (Hoste et al. 1998).
to 16 (Hoste et al. 1998).
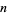 |
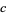 |
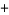 |
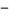 |
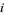 |
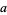 |
| Sloane | A051766 | A051767 | A051768 | A051769 | A052400 |
| 3 | 0 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 0 | 0 | 1 |
| 5 | 0 | 0 | 0 | 2 | 0 |
| 6 | 0 | 0 | 0 | 2 | 1 |
| 7 | 0 | 0 | 0 | 7 | 0 |
| 8 | 0 | 0 | 1 | 16 | 4 |
| 9 | 2 | 0 | 0 | 47 | 0 |
| 10 | 27 | 0 | 6 | 125 | 7 |
| 11 | 187 | 0 | 0 | 365 | 0 |
| 12 | 1103 | 1 | 40 | 1015 | 17 |
| 13 | 6919 | 0 | 0 | 3069 | 0 |
| 14 | 37885 | 6 | 227 | 8813 | 41 |
| 15 | 226580 | 0 | 1 | 26712 | 0 |
| 16 | 1308449 | 65 | 1361 | 78717 | 113 |
If a knot is amphichiral, the "amphichirality" is 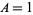 , otherwise
, otherwise 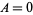 (Jones 1987). Arf invariants are designated
(Jones 1987). Arf invariants are designated 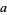 . Braid words are denoted
. Braid words are denoted 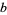 (Jones 1987). Conway's knot notation
(Jones 1987). Conway's knot notation 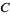 for knots up to 10 crossings is given by Rolfsen (1976). Hyperbolic volumes are given (Adams et al. 1991; Adams 1994). The braid index
for knots up to 10 crossings is given by Rolfsen (1976). Hyperbolic volumes are given (Adams et al. 1991; Adams 1994). The braid index 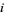 is given by Jones (1987). Alexander polynomials
is given by Jones (1987). Alexander polynomials 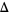 are given in Rolfsen (1976), but with the polynomials for 10-083 and 10-086 reversed (Jones 1987). The Alexander polynomials are normalized according to Conway, and given in abbreviated form
are given in Rolfsen (1976), but with the polynomials for 10-083 and 10-086 reversed (Jones 1987). The Alexander polynomials are normalized according to Conway, and given in abbreviated form 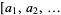 for
for 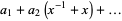 .
.
The Jones polynomials 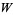 for knots of up to 10 crossings are given by Jones (1987), and the Jones polynomials
for knots of up to 10 crossings are given by Jones (1987), and the Jones polynomials 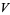 can be either computed from these, or taken from Adams (1994) for knots of up to 9 crossings (although most polynomials are associated with the wrong knot in the first printing). The Jones polynomials can be listed in the abbreviated form
can be either computed from these, or taken from Adams (1994) for knots of up to 9 crossings (although most polynomials are associated with the wrong knot in the first printing). The Jones polynomials can be listed in the abbreviated form 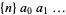 for
for 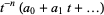 , and correspond either to the knot depicted by Rolfsen or its mirror image, whichever has the lower power of
, and correspond either to the knot depicted by Rolfsen or its mirror image, whichever has the lower power of 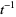 . The HOMFLY polynomial
. The HOMFLY polynomial 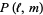 and Kauffman polynomial F(a,x) are given in Lickorish and Millett (1988) for knots of up to 7 crossings. M. B. Thistlethwaite has tabulated the HOMFLY polynomial and Kauffman polynomial F for knots of up to 13 crossings.
and Kauffman polynomial F(a,x) are given in Lickorish and Millett (1988) for knots of up to 7 crossings. M. B. Thistlethwaite has tabulated the HOMFLY polynomial and Kauffman polynomial F for knots of up to 13 crossings.
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 280-286, 1994.
Adams, C.; Hildebrand, M.; and Weeks, J. "Hyperbolic Invariants of Knots and Links." Trans. Amer. Math. Soc. 1, 1-56, 1991.
Alexander, J. W. and Briggs, G. B. "On Types of Knotted Curves." Ann. Math. 28, 562-586, 1927.
Aneziris, C. N. The Mystery of Knots: Computer Programming for Knot Tabulation. Singapore: World Scientific, 1999.
Ashley, C. W. The Ashley Book of Knots. New York: McGraw-Hill, 1996.
Bar-Natan, D. "The Mathematica Package KnotTheory.m." https://www.math.toronto.edu/~drorbn/KAtlas/Manual/.
Bar-Natan, D. "The Rolfsen Knot Table." https://www.math.toronto.edu/~drorbn/KAtlas/Knots/.
Bogomolny, A. "Knots...." https://www.cut-the-knot.org/do_you_know/knots.shtml.
Bruzelius, L. "Knots and Splices." https://pc-78-120.udac.se:8001/WWW/Nautica/Bibliography/Knots&Splices.html.
Caudron, A. "Classification des noeuds et des enlacements." Prepublication Math. d'Orsay. Orsay, France: Université Paris-Sud, 1980.
Cerf, C. "Atlas of Oriented Knots and Links." Topology Atlas Invited Contributions 3, No. 2, 1-32, 1998. https://at.yorku.ca/t/a/i/c/31.htm.
Cha, J. C. and Livingston, C. "KnotInfo: Table of Knot Invariants." https://www.indiana.edu/~knotinfo/.
Cha, J. C. and Livingston, C. "Unknown Values in the Table of Knots." 2008 May 16. https://arxiv.org/abs/math.GT/0503125.
Conway, J. H. "An Enumeration of Knots and Links." In Computational Problems in Abstract Algebra (Ed. J. Leech). Oxford, England: Pergamon Press, pp. 329-358, 1970.
Eppstein, D. "Knot Theory." https://www.ics.uci.edu/~eppstein/junkyard/knot.html.
Erdener, K.; Candy, C.; and Wu, D. "Verification and Extension of Topological Knot Tables." ftp://chs.cusd.claremont.edu/pub/knot/FinalReport.sit.hqx.
ERP Productions. "Ropers Knot Pages, Real Knots: Knotting, Bends and Hitches." https://www.realknots.com/.
GANG. "GANG Knot Library." https://www.gang.umass.edu/library/knots/.
Gordon, C. and Luecke, J. "Knots are Determined by their Complements." J. Amer. Math. Soc. 2, 371-415, 1989.
Haken, W. "Theorie der Normalflachen." Acta Math. 105, 245-375, 1961.
Hemion, G. "On the Classification of Homeomorphisms of 2-Manifolds and the Classification of 3-Manifolds." Acta Math. 142, 123-155, 1979.
Hoste, J.; Thistlethwaite, M.; and Weeks, J. "The First 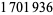 Knots." Math. Intell. 20, 33-48, Fall 1998.
Knots." Math. Intell. 20, 33-48, Fall 1998.
Jones, V. "Hecke Algebra Representations of Braid Groups and Link Polynomials." Ann. Math. 126, 335-388, 1987.
Kauffman, L. Knots and Applications. River Edge, NJ: World Scientific, 1995.
Kauffman, L. Knots and Physics. Teaneck, NJ: World Scientific, 1991.
Kirkman, T. P. "The Enumeration, Description, and Construction of Knots Fewer than Ten Crossings." Trans. Roy. Soc. Edinburgh 32, 1885, 281-309.
Kirkman, T. P. "The 634 Unifilar Knots of Ten Crossings Enumerated and Defined." Trans. Roy. Soc. Edinburgh 32, 483-506, 1885.
Korpegård, J. "The Knotting Dictionary of Kännet." https://www.korpegard.nu/knot/.
Lickorish, W. B. R. and Millett, B. R. "The New Polynomial Invariants of Knots and Links." Math. Mag. 61, 1-23, 1988.
Listing, J. B. "Vorstudien zur Topologie." Göttingen Studien, University of Göttingen, Germany, 1848.
Little, C. N. "On Knots, with a Census of Order Ten." Trans. Connecticut Acad. Sci. 18, 374-378, 1885.
Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., 1993.
Murasugi, K. and Kurpita, B. I. A Study of Braids. Dordrecht, Netherlands: Kluwer, 1999.
Neuwirth, L. "The Theory of Knots." Sci. Amer. 140, 84-96, Jun. 1979.
Perko, K. "Invariants of 11-Crossing Knots." Prepublications Math. d'Orsay. Orsay, France: Université Paris-Sub, 1980.
Perko, K. "Primality of Certain Knots." Topology Proc. 7, 109-118, 1982.
Praslov, V. V. and Sossinsky, A. B. Knots, Links, Braids and 3-Manifolds: An Introduction to the New Invariants in Low-Dimensional Topology. Providence, RI: Amer. Math. Soc., 1996.
Przytycki, J. "A History of Knot Theory from Vandermonde to Jones." Proc. Mexican Nat. Congress Math., Nov. 1991.
Reidemeister, K. Knotentheorie. Berlin: Springer-Verlag, 1932.
Rolfsen, D. "Table of Knots and Links." Appendix C in Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 280-287, 1976.
Schubert, H. Sitzungsber. Heidelberger Akad. Wiss., Math.-Naturwiss. Klasse, 3rd Abhandlung. 1949.
Sloane, N. J. A. Sequences A002863/M0851 and A086825 in "The On-Line Encyclopedia of Integer Sequences."
Sloane, N. J. A. and Plouffe, S. Figure M0851 in The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Stoimenow, A. "Polynomials of Knots with Up to 10 Crossings." Rev. March 9, 2002. https://www.math.toronto.edu/stoimeno/poly.ps.gz.
Suber, O. "Knots on the Web." https://www.earlham.edu/~peters/knotlink.htm.
Tait, P. G. "On Knots I, II, and III." Scientific Papers, Vol. 1. Cambridge, England: University Press, pp. 273-347, 1898.
Thistlethwaite, M. B. "Knot Tabulations and Related Topics." In Aspects of Topology in Memory of Hugh Dowker 1912-1982 (Ed. I. M. James and E. H. Kronheimer). Cambridge, England: Cambridge University Press, pp. 2-76, 1985.
Thistlethwaite, M. B. ftp://chs.cusd.claremont.edu/pub/knot/Thistlethwaite_Tables/.
Thistlethwaite, M. B. "Morwen's Home Page." https://www.math.utk.edu/~morwen/.
Thompson, W. T. "On Vortex Atoms." Philos. Mag. 34, 15-24, 1867.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 132-135, 1991.
Weisstein, E. W. "Books about Knot Theory." https://www.ericweisstein.com/encyclopedias/books/KnotTheory.html.
Zia. "Zia Knotting." https://204.30.30.10/hac/knots/



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة توجه دعوة لجامعة القادسية للمشاركة في حفل التخرج المركزي
|
|
|