Chi-Squared Test

Let the probabilities of various classes in a distribution be 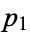, , 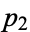..., 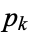, with observed frequencies 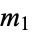, , 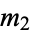..., 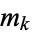. The quantity

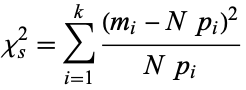(1)

is therefore a measure of the deviation of a sample from expectation, where 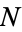 is the sample size. Karl Pearson proved that the limiting distribution of  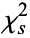is a chi-squared distribution (Kenney and Keeping 1951, pp. 114-116).

The probability that the distribution assumes a value of 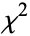 greater than the measured value  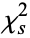is then given by

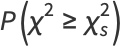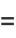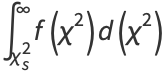			(2)
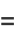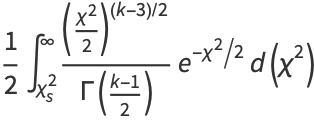			(3)
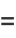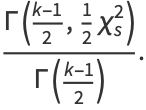			(4)

There are some subtleties involved in using the 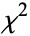 test to fit curves (Kenney and Keeping 1951, pp. 118-119). When fitting a one-parameter solution using 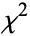, the best-fit parameter value can be found by calculating  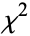at three points, plotting against the parameter values of these points, then finding the minimum of a parabola fit through the points (Cuzzi 1972, pp. 162-168).

REFERENCES:

Cuzzi, J. The Subsurface Nature of Mercury and Mars from Thermal Microwave Emission. Ph.D. Thesis. Pasadena, CA: California Institute of Technology, 1972.

Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.