


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-4-2021
Date: 4-3-2021
Date: 22-3-2021
|
A Poisson process is a process satisfying the following properties:
1. The numbers of changes in nonoverlapping intervals are independent for all intervals.
2. The probability of exactly one change in a sufficiently small interval 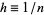 is
is 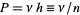 , where
, where  is the probability of one change and
is the probability of one change and 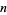 is the number of trials.
is the number of trials.
3. The probability of two or more changes in a sufficiently small interval 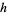 is essentially 0.
is essentially 0.
In the limit of the number of trials becoming large, the resulting distribution is called a Poisson distribution.
REFERENCES:
Grimmett, G. and Stirzaker, D. Probability and Random Processes, 2nd ed. Oxford, England: Oxford University Press, 1992.
Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 548-549, 1984.
Ross, S. M. Stochastic Processes, 2nd ed. New York: Wiley, p. 59, 1996.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|