


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-2-2021
Date: 10-2-2021
Date: 27-4-2021
|
Given a sample of 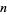 variates
variates 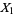 , ...,
, ..., 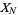 , reorder them so that
, reorder them so that 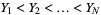 . Then
. Then 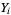 is called the
is called the 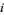 th order statistic (Hogg and Craig 1970, p. 146), sometimes also denoted
th order statistic (Hogg and Craig 1970, p. 146), sometimes also denoted 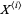 . Special cases include the minimum
. Special cases include the minimum
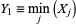 |
(1) |
and maximum
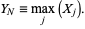 |
(2) |
Important functions of order statistics include the statistical range
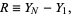 |
(3) |
midrange
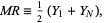 |
(4) |
and statistical median
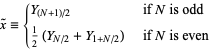 |
(5) |
(Hogg and Craig 1970, p. 152).
If 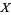 has probability density function
has probability density function 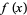 and distribution function
and distribution function 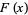 , then the probability function of
, then the probability function of 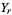 is given by
is given by
![f_(Y_r)=(N!)/((r-1)!(N-r)!)[F(x)]^(r-1)[1-F(x)]^(N-r)f(x)](https://mathworld.wolfram.com/images/equations/OrderStatistic/NumberedEquation6.gif) |
(6) |
for 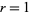 , ...,
, ..., 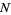 (Rose and Smith 2002, pp. 311 and 454).
(Rose and Smith 2002, pp. 311 and 454).
A robust estimation technique based on linear combinations of order statistics is called an L-estimate.
REFERENCES:
Balakrishnan, N. and Chen, W. W. S. Handbook of Tables for Order Statistics from Lognormal Distributions with Applications. Amsterdam, Netherlands: Kluwer, 1999.
Balakrishnan, N. and Cohen, A. C. Order Statistics and Inference. New York: Academic Press, 1991.
Balakrishnan, N. and Rao, C. R. (Eds.). Handbook of Statistics, Vol. 16: Order Statistics: Theory and Methods. Amsterdam, Netherlands: Elsevier, 1998.
Balakrishnan, N. and Rao, C. R. (Eds.). Order Statistics: Applications. Amsterdam, Netherlands: Elsevier, 1998.
David, H. A. Order Statistics, 2nd ed. New York: Wiley, 1981.
Gibbons, J. D. and Chakraborti, S. (Eds.). Nonparametric Statistic Inference, 3rd ed. exp. rev. New York: Dekker, 1992.
Hogg, R. V. and Craig, A. T. Introduction to Mathematical Statistics, 3rd ed. New York: Macmillan, 1970.
Rose, C. and Smith, M. D. "Order Statistics." §9.4 in Mathematical Statistics with Mathematica. New York: Springer-Verlag, pp. 311-322, 2002.
Rose, C. and Smith, M. D. "Computational Order Statistics." Mathematica J. 9, 790-802, 2005.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|