المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Statistical Range |
 1088
 05:24 مساءً
date: 10-2-2021 |
Author : Feller, W. 
Book or Source : An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, 1968. 
Page and Part : ...|
Read More
Date: 8-2-2021
1282
Date: 4-5-2021
4086
Date: 20-4-2021
1088
|
The term "range" has two completely different meanings in statistics.
Given order statistics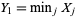 
, 
, ..., 
, 
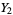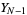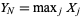, the range of the random sample is defined by
 |
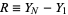(1) |
(Hogg and Craig 1995, p. 152).
For small samples, the range is a good estimator of the population standard deviation (Kenney and Keeping 1962, pp. 213-214).
For a continuous uniform distribution
 |
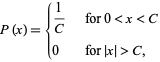(2) |
the distribution of the range is given by
 |
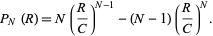(3) |
This is illustrated above for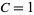 
and values of 
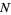from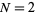 
(red) to 
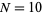(violet).
Given two samples with sizes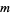 
and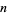 
and ranges 
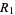and 
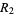, let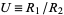 
. Then
![D(u)={(m(m-1)n(n-1))/((m+n)(m+n-1)(m+n-2))[(m+n)u^(m-2)-(m+n-2)u^(m-1)]; for 0<=u<=1; (m(m-1)n(n-1))/((m+n)(m+n-1)(m+n-2))[(m+n)u^(-n)-(m+n-2)u^(-n-1)]; for 1<=u<infty.](https://mathworld.wolfram.com/images/equations/StatisticalRange/NumberedEquation4.gif) |
(4) |
The mean is
 |
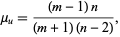(5) |
and the mode is
 |
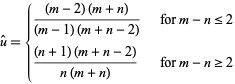(6) |
(Kenney and Keeping 1962).
REFERENCES:
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, 1968.
Hogg, R. V. and Craig, A. T. Introduction to Mathematical Statistics, 5th ed. New York: Macmillan, p. 152, 1995.
Kenney, J. F. and Keeping, E. S. "The Range." §6.2 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 75-76, 213-214, 1962.
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
