


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-2-2021
Date: 1-5-2021
Date: 6-4-2021
|
The correlation coefficient, sometimes also called the cross-correlation coefficient, Pearson correlation coefficient (PCC), Pearson's 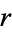 , the Perason product-moment correlation coefficient (PPMCC), or the bivariate correlation, is a quantity that gives the quality of a least squares fitting to the original data. To define the correlation coefficient, first consider the sum of squared values
, the Perason product-moment correlation coefficient (PPMCC), or the bivariate correlation, is a quantity that gives the quality of a least squares fitting to the original data. To define the correlation coefficient, first consider the sum of squared values 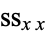 ,
, 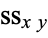 , and
, and 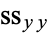 of a set of
of a set of 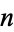 data points
data points 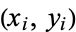 about their respective means,
about their respective means,
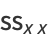 |
 |
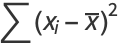 |
(1) |
 |
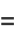 |
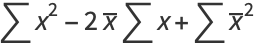 |
(2) |
 |
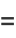 |
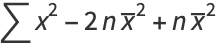 |
(3) |
 |
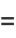 |
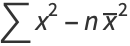 |
(4) |
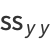 |
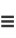 |
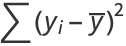 |
(5) |
 |
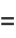 |
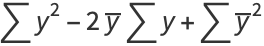 |
(6) |
 |
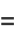 |
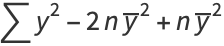 |
(7) |
 |
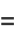 |
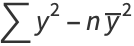 |
(8) |
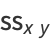 |
 |
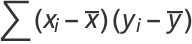 |
(9) |
 |
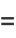 |
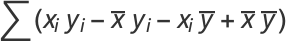 |
(10) |
 |
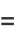 |
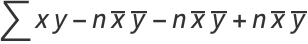 |
(11) |
 |
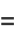 |
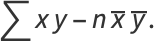 |
(12) |
These quantities are simply unnormalized forms of the variances and covariance of 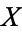 and
and 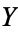 given by
given by
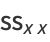 |
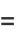 |
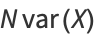 |
(13) |
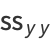 |
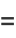 |
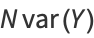 |
(14) |
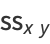 |
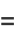 |
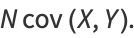 |
(15) |
For linear least squares fitting, the coefficient 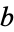 in
in
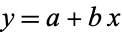 |
(16) |
is given by
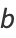 |
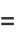 |
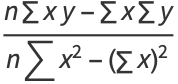 |
(17) |
 |
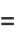 |
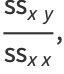 |
(18) |
and the coefficient 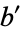 in
in
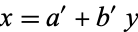 |
(19) |
is given by
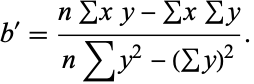 |
(20) |

The correlation coefficient 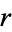 (sometimes also denoted
(sometimes also denoted 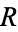 ) is then defined by
) is then defined by
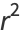 |
 |
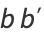 |
(21) |
 |
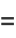 |
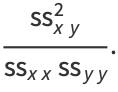 |
(22) |
The correlation coefficient is also known as the product-moment coefficient of correlation or Pearson's correlation. The correlation coefficients for linear fits to increasingly noisy data are shown above.
The correlation coefficient has an important physical interpretation. To see this, define
![A=[sumx^2-nx^_^2]^(-1)](https://mathworld.wolfram.com/images/equations/CorrelationCoefficient/NumberedEquation4.gif) |
(23) |
and denote the "expected" value for 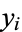 as
as 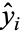 . Sums of
. Sums of 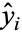 are then
are then
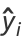 |
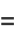 |
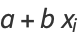 |
(24) |
 |
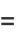 |
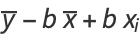 |
(25) |
 |
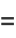 |
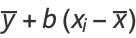 |
(26) |
 |
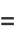 |
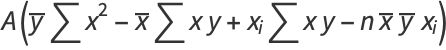 |
(27) |
 |
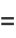 |
![A[y^_sumx^2+(x_i-x^_)sumxy-nx^_y^_x_i]](https://mathworld.wolfram.com/images/equations/CorrelationCoefficient/Inline87.gif) |
(28) |
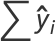 |
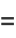 |
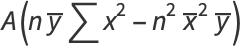 |
(29) |
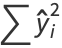 |
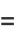 |
![A^2[ny^_^2(sumx^2)^2-n^2x^_^2y^_^2(sumx^2)-2nx^_y^_(sumxy)(sumx^2)+2n^2x^_^3y^_(sumxy)+(sumx^2)(sumxy)^2-nx^_^2(sumxy)]](https://mathworld.wolfram.com/images/equations/CorrelationCoefficient/Inline93.gif) |
(30) |
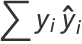 |
 |
![Asum[y_iy^_sumx^2+y_i(x_i-x^_)sumxy-nx^_y^_x_iy_i]](https://mathworld.wolfram.com/images/equations/CorrelationCoefficient/Inline96.gif) |
(31) |
 |
 |
![A[ny^_^2sumx^2+(sumxy)^2-nx^_y^_sumxy-nx^_y^_(sumxy)]](https://mathworld.wolfram.com/images/equations/CorrelationCoefficient/Inline99.gif) |
(32) |
 |
 |
![A[ny^_^2sumx^2+(sumxy)^2-2nx^_y^_sumxy].](https://mathworld.wolfram.com/images/equations/CorrelationCoefficient/Inline102.gif) |
(33) |
The sum of squared errors is then
 |
 |
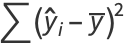 |
(34) |
 |
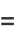 |
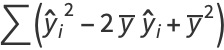 |
(35) |
 |
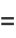 |
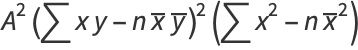 |
(36) |
 |
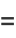 |
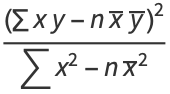 |
(37) |
 |
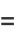 |
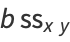 |
(38) |
 |
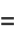 |
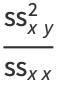 |
(39) |
 |
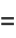 |
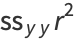 |
(40) |
 |
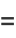 |
 |
(41) |
and the sum of squared residuals is
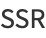 |
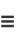 |
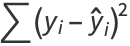 |
(42) |
 |
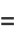 |
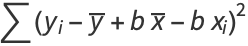 |
(43) |
 |
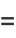 |
![sum[y_i-y^_-b(x_i-x^_)]^2](https://mathworld.wolfram.com/images/equations/CorrelationCoefficient/Inline135.gif) |
(44) |
 |
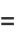 |
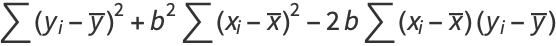 |
(45) |
 |
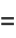 |
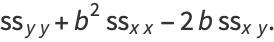 |
(46) |
But
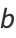 |
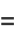 |
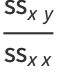 |
(47) |
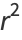 |
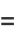 |
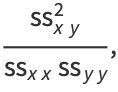 |
(48) |
so
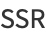 |
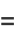 |
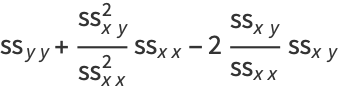 |
(49) |
 |
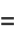 |
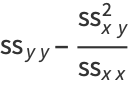 |
(50) |
 |
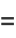 |
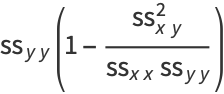 |
(51) |
 |
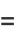 |
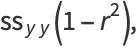 |
(52) |
and
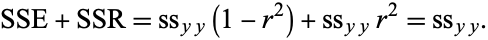 |
(53) |
The square of the correlation coefficient 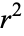 is therefore given by
is therefore given by
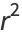 |
 |
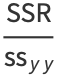 |
(54) |
 |
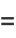 |
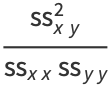 |
(55) |
 |
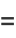 |
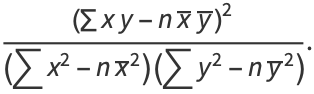 |
(56) |
In other words, 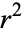 is the proportion of
is the proportion of 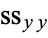 which is accounted for by the regression.
which is accounted for by the regression.
If there is complete correlation, then the lines obtained by solving for best-fit 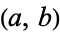 and
and 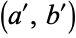 coincide (since all data points lie on them), so solving (◇) for
coincide (since all data points lie on them), so solving (◇) for 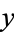 and equating to (◇) gives
and equating to (◇) gives
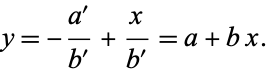 |
(57) |
Therefore, 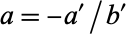 and
and 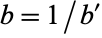 , giving
, giving
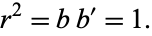 |
(58) |
The correlation coefficient is independent of both origin and scale, so
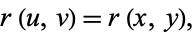 |
(59) |
where
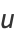 |
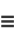 |
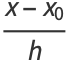 |
(60) |
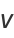 |
 |
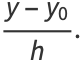 |
(61) |
REFERENCES:
Acton, F. S. Analysis of Straight-Line Data. New York: Dover, 1966.
Edwards, A. L. "The Correlation Coefficient." Ch. 4 in An Introduction to Linear Regression and Correlation. San Francisco, CA: W. H. Freeman, pp. 33-46, 1976.
Gonick, L. and Smith, W. "Regression." Ch. 11 in The Cartoon Guide to Statistics. New York: Harper Perennial, pp. 187-210, 1993.
Kenney, J. F. and Keeping, E. S. "Linear Regression and Correlation." Ch. 15 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 252-285, 1962.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Linear Correlation." §14.5 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 630-633, 1992.
Snedecor, G. W. and Cochran, W. G. "The Sample Correlation Coefficient 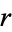 " and "Properties of
" and "Properties of 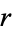 ." §10.1-10.2 in Statistical Methods, 7th ed. Ames, IA: Iowa State Press, pp. 175-178, 1980.
." §10.1-10.2 in Statistical Methods, 7th ed. Ames, IA: Iowa State Press, pp. 175-178, 1980.
Spiegel, M. R. "Correlation Theory." Ch. 14 in Theory and Problems of Probability and Statistics, 2nd ed. New York: McGraw-Hill, pp. 294-323, 1992.
Whittaker, E. T. and Robinson, G. "The Coefficient of Correlation for Frequency Distributions which are not Normal." §166 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 334-336, 1967.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|