


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-2-2021
Date: 25-4-2021
Date: 15-2-2021
|
Consider the sample standard deviation
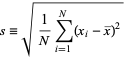 |
(1) |
for 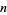 samples taken from a population with a normal distribution. The distribution of
samples taken from a population with a normal distribution. The distribution of 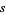 is then given by
is then given by
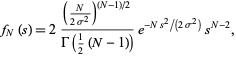 |
(2) |
where 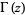 is a gamma function and
is a gamma function and
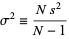 |
(3) |
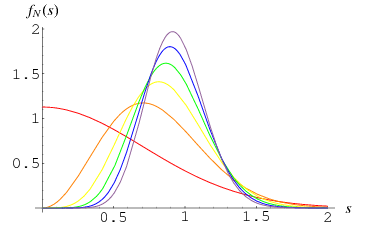
(Kenney and Keeping 1951, pp. 161 and 171). The function 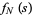 is plotted above for
is plotted above for 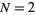 (red), 4 (orange), ..., 10 (blue), and 12 (violet).
(red), 4 (orange), ..., 10 (blue), and 12 (violet).
The mean is given by
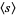 |
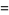 |
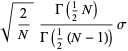 |
(4) |
 |
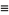 |
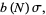 |
(5) |
where
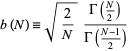 |
(6) |
(Kenney and Keeping 1951, p. 171). The function 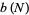 is known as
is known as 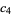 in statistical process control (Duncan 1986, pp. 62 and 134). Romanovsky showed that
in statistical process control (Duncan 1986, pp. 62 and 134). Romanovsky showed that
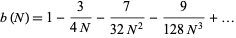 |
(7) |
(OEIS A088801 and A088802; Romanovsky 1925; Pearson 1935; Kenney and Keeping 1951, p. 171).
The raw moments are given by
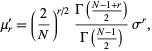 |
(8) |
and the variance of 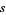 is
is
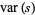 |
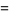 |
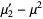 |
(9) |
 |
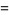 |
![1/N[N-1-(2Gamma^2(N/2))/(Gamma^2((N-1)/2))]sigma^2.](https://mathworld.wolfram.com/images/equations/StandardDeviationDistribution/Inline20.gif) |
(10) |
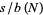 is an unbiased estimator of
is an unbiased estimator of 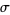 (Kenney and Keeping 1951, p. 171).
(Kenney and Keeping 1951, p. 171).
REFERENCES:
Duncan, A. J. Quality Control and Industrial Statistics, 5th ed. New York: McGraw-Hill, 1986.
Kenney, J. F. and Keeping, E. S. "The Distribution of the Standard Deviation." §7.8 in Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, pp. 170-173, 1951.
Pearson, E. The Application of Statistical Methods to Industrial Standardization and Quality Control. British Standards House, 1935.
Romanovsky, V. "On the Moments of the Standard Deviation and of the Correlation Coefficient in Samples from Normal." Metron 5, 3-46, 1925.
Sloane, N. J. A. Sequences A088801 and A088802 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|