


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-4-2021
Date: 17-3-2021
Date: 6-2-2016
|
When computing the sample variance 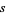 numerically, the mean must be computed before
numerically, the mean must be computed before 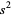 can be determined. This requires storing the set of sample values. However, it is possible to calculate
can be determined. This requires storing the set of sample values. However, it is possible to calculate 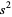 using a recursion relationship involving only the last sample as follows. This means
using a recursion relationship involving only the last sample as follows. This means 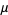 itself need not be precomputed, and only a running set of values need be stored at each step.
itself need not be precomputed, and only a running set of values need be stored at each step.
In the following, use the somewhat less than optimal notation 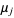 to denote
to denote 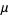 calculated from the first
calculated from the first 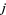 samples (i.e., not the
samples (i.e., not the 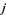 th moment)
th moment)
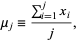 |
(1) |
and let 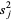 denotes the value for the bias-corrected sample variance
denotes the value for the bias-corrected sample variance 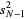 calculated from the first
calculated from the first 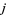 samples. The first few values calculated for the mean are
samples. The first few values calculated for the mean are
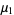 |
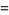 |
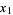 |
(2) |
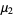 |
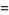 |
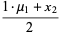 |
(3) |
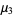 |
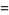 |
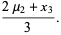 |
(4) |
Therefore, for 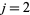 , 3 it is true that
, 3 it is true that
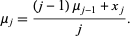 |
(5) |
Therefore, by induction,
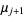 |
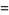 |
![([(j+1)-1]mu_((j+1)-1)+x_(j+1))/(j+1)](https://mathworld.wolfram.com/images/equations/SampleVarianceComputation/Inline24.gif) |
(6) |
 |
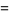 |
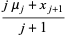 |
(7) |
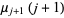 |
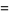 |
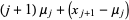 |
(8) |
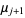 |
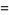 |
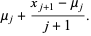 |
(9) |
By the definition of the sample variance,
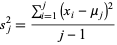 |
(10) |
for 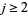 . Defining
. Defining 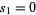 ,
, 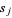 can then be computed using the recurrence equation
can then be computed using the recurrence equation
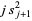 |
 |
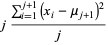 |
(11) |
 |
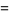 |
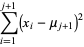 |
(12) |
 |
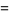 |
![sum_(i=1)^(j+1)[(x_i-mu_j)+(mu_j-mu_(j+1))]^2](https://mathworld.wolfram.com/images/equations/SampleVarianceComputation/Inline45.gif) |
(13) |
 |
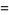 |
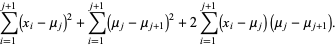 |
(14) |
Working on the first term,
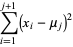 |
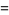 |
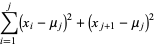 |
(15) |
 |
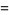 |
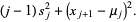 |
(16) |
Use (◇) to write
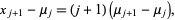 |
(17) |
so
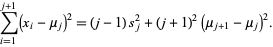 |
(18) |
Now work on the second term in (◇),
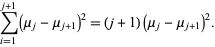 |
(19) |
Considering the third term in (◇),
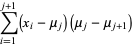 |
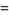 |
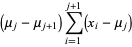 |
(20) |
 |
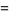 |
![(mu_j-mu_(j+1))[sum_(i=1)^(j)(x_i-mu_j)+(x_(j+1)-mu_j)]](https://mathworld.wolfram.com/images/equations/SampleVarianceComputation/Inline60.gif) |
(21) |
 |
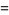 |
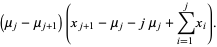 |
(22) |
But
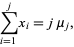 |
(23) |
so
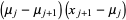 |
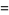 |
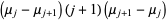 |
(24) |
 |
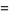 |
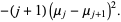 |
(25) |
Finally, plugging (◇), (◇), and (◇) into (◇),
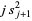 |
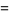 |
![[(j-1)s_j^2+(j+1)^2(mu_(j+1)-mu_j)^2]+[(j+1)(mu_j-mu_(j+1))^2]+2[-(j+1)(mu_j-mu_(j+1))^2]](https://mathworld.wolfram.com/images/equations/SampleVarianceComputation/Inline72.gif) |
(26) |
 |
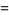 |
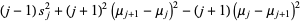 |
(27) |
 |
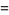 |
-mu_j)^2](https://mathworld.wolfram.com/images/equations/SampleVarianceComputation/Inline78.gif) |
(28) |
 |
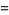 |
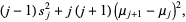 |
(29) |
gives the desired expression for 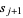 in terms of
in terms of 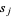 ,
, 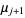 , and
, and 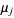 ,
,
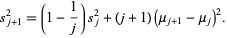 |



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|