
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-10-2020
Date: 24-10-2020
Date: 10-9-2020
|
A number 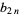 having generating function
having generating function
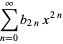 |
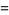 |
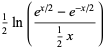 |
(1) |
 |
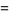 |
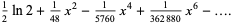 |
(2) |
For 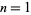 , 2, ..., the denominators are 48, 5760, 362880, 19353600, ... (OEIS A057868).
, 2, ..., the denominators are 48, 5760, 362880, 19353600, ... (OEIS A057868).
It has closed form
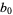 |
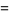 |
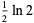 |
(3) |
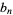 |
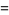 |
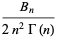 |
(4) |
and 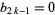 , where
, where 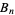 is a Bernoulli number and
is a Bernoulli number and 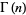 a gamma function.
a gamma function.
REFERENCES:
Sloane, N. J. A. Sequence A057868 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
مكتبة العتبة العباسية.. خدمات رقمية متطورة وجهود لتلبية احتياجات الباحثين
|
|
|