


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-6-2020
Date: 17-12-2019
Date: 21-3-2020
|
Find a way to stack a square of cannonballs laid out on the ground into a square pyramid (i.e., find a square number which is also square pyramidal). This corresponds to solving the Diophantine equation
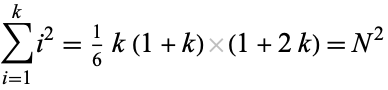 |
for some pyramid height 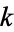 .
.
The only solutions are 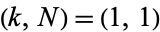 and
and 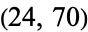 (Ball and Coxeter 1987, Dickson 2005), as conjectured by Lucas (1875), partially proved by Moret-Blanc (1876) and Lucas (1877), and proved by Watson (1918). Watson's proof was almost elementary, disposing of most cases by elementary means, but resorting to the use of elliptic functions for one pesky case. Entirely elementary proofs have been given by Ma (1985) and Anglin (1990).
(Ball and Coxeter 1987, Dickson 2005), as conjectured by Lucas (1875), partially proved by Moret-Blanc (1876) and Lucas (1877), and proved by Watson (1918). Watson's proof was almost elementary, disposing of most cases by elementary means, but resorting to the use of elliptic functions for one pesky case. Entirely elementary proofs have been given by Ma (1985) and Anglin (1990).
REFERENCES:
Anglin, W. S. "The Square Pyramid Puzzle." Amer. Math. Monthly 97, 120-124, 1990.
Anglin, W. S. The Queen of Mathematics: An Introduction to Number Theory. Dordrecht, Netherlands: Kluwer, 1995.
Baker, A. and Davenport, H. "The Equations 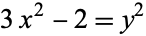 and
and 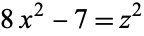 ." Quart J. Math. Ser. 2 20, 129-137, 1969.
." Quart J. Math. Ser. 2 20, 129-137, 1969.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 59, 1987.
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, p. 25, 2005.
Kanagasabapathy, P. and Ponnudurai, T. "The Simultaneous Diophantine Equations 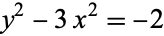 and
and 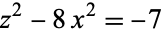 ." Quart. J. Math. Ser. 2 26, 275-278, 1975.
." Quart. J. Math. Ser. 2 26, 275-278, 1975.
Ljunggren, W. "New Solution of a Problem Posed by E. Lucas." Nordisk Mat. Tidskrift 34, 65-72, 1952.
Lucas, É. Question 1180. Nouv. Ann. Math. Ser. 2 14, 336, 1875.
Lucas, É. Solution de Question 1180. Nouv. Ann. Math. Ser. 2 15, 429-432, 1877.
Ma, D. G. "An Elementary Proof of the Solutions to the Diophantine Equation 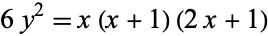 ." Sichuan Daxue Xuebao, No. 4, 107-116, 1985.
." Sichuan Daxue Xuebao, No. 4, 107-116, 1985.
Moret-Blanc, M. Question 1180. Nouv. Ann. Math. Ser. 2 15, 46-48, 1876.
Ogilvy, C. S. and Anderson, J. T. Excursions in Number Theory. New York: Dover, pp. 77 and 152, 1988.
Pappas, T. "Cannon Balls & Pyramids." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 93, 1989.
Watson, G. N. "The Problem of the Square Pyramid." Messenger. Math. 48, 1-22, 1918.



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
نشر مظاهر الفرح في مرقد أبي الفضل العباس بذكرى ولادة السيدة زينب (عليهما السلام)
|
|
|