Keith Number

A Keith number is an 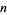-digit integer  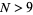such that if a Fibonacci-like sequence (in which each term in the sequence is the sum of the  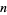previous terms) is formed with the first  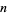terms taken as the decimal digits of the number 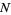, then  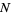itself occurs as a term in the sequence. For example, 197 is a Keith number since it generates the sequence 1, 9, 7, 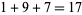, , 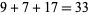, , 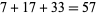, 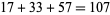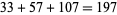... (Keith). Keith numbers are also called repfigit (repetitive fibonacci-like digit) numbers.

There is no known general technique for finding Keith numbers except by exhaustive search. Keith numbers are much rarer than the primes, with only 84 Keith numbers with 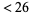 digits. The first few are 14, 19, 28, 47, 61, 75, 197, 742, 1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909, ... (OEIS A007629). As of Mar. 31, 2006, there are 95 known Keith numbers (Keith). The number of Keith numbers having 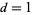, 2, ... digits are 0, 6, 2, 9, 7, 10, 2, 3, 2, 0, 2, 4, 2, 3, 3, 3, 5, 3, 5, 3, 1, 1, 3, 1, 1, 3, 7, 1, 2, 5, 2, 4, 6, 3, ... (OEIS A050235), as summarized in the following table.

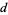	-digit Keith numbers
2	14, 19, 28, 47, 61, 75
3	197, 742
4	1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909
5	31331, 34285, 34348, 55604, 62662, 86935, 93993
6	120284, 129106, 147640, 156146, 174680, 183186, 298320, 355419, 694280, 925993
7	1084051, 7913837
8	11436171, 33445755, 44121607
9	129572008, 251133297
10	(none)
11	24769286411 96189170155
12	171570159070, 202366307758, 239143607789, 296658839738
13	1934197506555, 8756963649152
14	43520999798747, 74596893730427, 97295849958669
15	120984833091531, 270585509032586, 754788753590897
16	3621344088074041, 3756915124022254, 4362827422508274
17	11812665388886672, 14508137312404344, 16402582054271374, 69953250322018194, 73583709853303061
18	119115440241433462, 166308721919462318, 301273478581322148
19	1362353777290081176, 3389041747878384662, 5710594497265802190, 5776750370944624064, 6195637556095764016
20	12763314479461384279, 27847652577905793413, 45419266414495601903
21	855191324330802397989
22	7657230882259548723593
23	26842994422637112523337, 36899277593852609997403, 61333853602129819189668
24	229146413136585558461227
25	9838678687915198599200604
26	18354972585225358067718266, 19876234926457288511947945, 98938191214220718050301312
27	153669354455482560987178342, 154677881401007799974564336, 133118411174059688391045955, 154140275428339949899922650, 295768237361291708645227474, 956633720464114515890318410, 988242310393860390066911414
28	9493976840390265868522067200
29	41796205765147426974704791528, 70267375510207885242218837404
30	127304146123884420932123248317, 389939548933846065763772833753, 344669719564188054170496150677, 756672276587447504826932994366, 534139807526361917710268232010
31	1598187483427964679092074853838, 2405620130870553672640058975437
32	41030306579725050560909919549414, 47824404246899742508216679149392, 42983394195992223818343905028410, 89980815134051887612993101615858
33	172451142646837728336412943204299, 193962639439026709638083447831059, 381933008901296879565658130750756, 359253598248137147666007355623218, 303294117104027490007126494842828, 312736110821858321305917486145434
34	1876178467884883559985053635963437, 2787674840304510129398176411111966, 5752090994058710841670361653731519

It is not known if there are an infinite number of Keith numbers.

The known prime Keith numbers are 19, 47, 61, 197, 1084051, 74596893730427, ... (OEIS A048970).

The 26-digit Keith number 98938191214220718050301312 was found in 2004 by D. Lichtblau using integer linear programming to solve the relevant Diophantine equations in the Wolfram Language. D. Lichtblau found all 30- and 31-digit Keith numbers on Jun. 23, 2009, and all 32-, 33-, and 34-digit Keith numbers on Aug. 26, 2009. The largest of these is 5752090994058710841670361653731519, which is the largest Keith number known as of August 2009.

Similarly, a reverse Keith, or revrepfigit (reverse replicating Fibonacci-like digit) number, is an 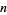-digit integer  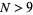such that if a Fibonacci-like sequence (in which each term in the sequence is the sum of the previous terms) is formed with the first terms taken as the decimal digits of the number 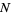, then the reversal of  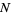occurs as a term in the sequence. For example, 341 is a revrepfigit since it generates the sequence 3, 4, 1, , , , , , .

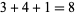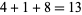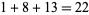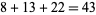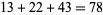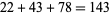The currently known revrepfigits are 12, 24, 36, 48, 52, 71, 341, 682, 1285, 5532, 8166, 17593, 28421, 74733, 90711, 759664, 901921, 1593583, 4808691, 6615651, 6738984, 8366363, 8422611, 26435142, 54734431, 57133931, 79112422, 351247542, 428899438, 489044741, 578989902, 3207761244, 4156222103, 5426705064, 5785766973, 6336657062, 48980740972, 51149725354, 83626284302, 94183600081, 98665175305, 1935391095868, 6002181268035, 6334708806271, 12348924235856, 27488180694681, 76365591939888, 309217509306732, 352062080376812, 714692062325732, 723735537269331, 2437358882180001, 6792079280704301, 62244424802562056, 203414193894268461, 217049132946408803, 415499563488189604, 561624665953167171, ... (OEIS A097060; A. Vrba, pers. comm., Dec. 28, 2006). Notice there are no numbers ending with zeros; they are not permitted since the zeros would be dropped upon reversal. But terms with internal zeros such as 90711 are allowed. The known prime revrepfigits are 71, 1593583, and 54734431 (A. Vrba, pers. comm,., Dec. 28, 2006).

It is not known if there are infinitely many revrepfigit numbers.

REFERENCES:

Esche, H. A. "Non-Decimal Replicating Fibonacci Digits." J. Recr. Math. 26, 193-194, 1994.

Heleen, B. "Finding Repfigits--A New Approach." J. Recr. Math. 26, 184-187, 1994.

Keith, M. "Repfigit Numbers." J. Recr. Math. 19, 41-42, 1987.

Keith, M. "All Repfigit Numbers Less than 100 Billion (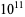)." J. Recr. Math. 26, 181-184, 1994.

Keith, M. "Keith Numbers." https://users.aol.com/s6sj7gt/mikekeit.htm.

Keith, M. "Determination of All Keith Numbers Up to 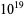." https://users.aol.com/s6sj7gt/keithnum.htm.

Lichtblau, D. "Solving Knapsack and Related Problems." International Mathematica Symposium 2004. Banff, Canada, 2004.

Pickover, C. "All Known Replicating Fibonacci Digits Less than One Billion." J. Recr. Math. 22, 176, 1990.

Piele, D. "Mathematica Pearls: Keith Numbers." Mathematica Res. Educ. 6, No. 3, 50-52, 1997.

Piele, D. "Mathematica Pearls: Keith Numbers." Mathematica Res. Educ. 7, No. 1, 44-45, 1998.

Robinson, N. M. "All Known Replicating Fibonacci Digits Less than One Thousand Billion (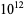)." J. Recr. Math. 26, 188-191, 1994.

Sherriff, K. "Computing Replicating Fibonacci Digits." J. Recr. Math. 26, 191-193, 1994.

Sloane, N. J. A. Sequences A007629, A048970, A050235, and A097060 in "The On-Line Encyclopedia of Integer Sequences."

"Table: Repfigit Numbers (Base 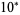) Less than 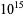." J. Recr. Math. 26, 195, 1994.