


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-6-2020
Date: 28-4-2020
Date: 20-4-2020
|
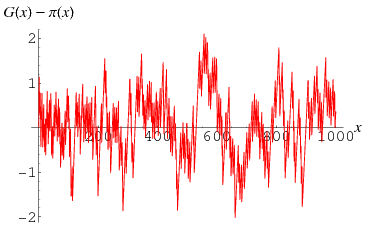
The Gram series is an approximation to the prime counting function given by
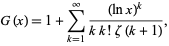 |
(1) |
where 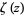 is the Riemann zeta function (Hardy 1999, p. 24). This approximation is 10 times better than
is the Riemann zeta function (Hardy 1999, p. 24). This approximation is 10 times better than 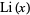 for
for 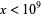 but has been proven to be worse infinitely often by Littlewood (Ingham 1990).
but has been proven to be worse infinitely often by Littlewood (Ingham 1990).
The Gram series is equivalent to the Riemann prime counting function (Hardy 1999, pp. 24-25)
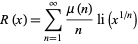 |
(2) |
where 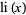 is the logarithmic integral and
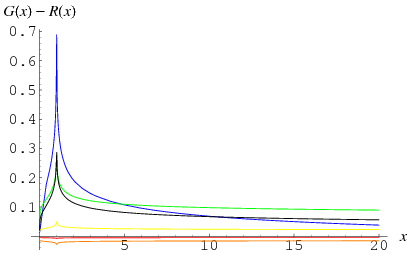
is the logarithmic integral and 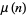 is the Möbius function (Hardy 1999, pp. 16 and 23; Borwein et al. 2000), but is much more tractable for numeric computations. For example, the plots above show the difference
is the Möbius function (Hardy 1999, pp. 16 and 23; Borwein et al. 2000), but is much more tractable for numeric computations. For example, the plots above show the difference 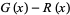 where
where 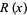 is computed using the Wolfram Language's built-in NSum command (black) and approximated using the first
is computed using the Wolfram Language's built-in NSum command (black) and approximated using the first 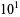 (blue),
(blue), 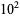 (green),
(green), 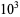 (yellow),
(yellow), 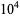 (orange), and
(orange), and 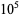 (red) points.
(red) points.
A related series due to Ramanujan is
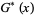 |
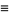 |
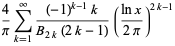 |
(3) |
 |
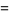 |
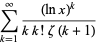 |
(4) |
 |
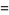 |
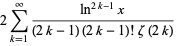 |
(5) |
 |
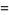 |
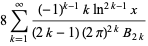 |
(6) |
(Berndt 1994, p. 124; Hardy 1999, p. 23), where 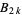 is a Bernoulli number. The integral analog, also found by Ramanujan, is
is a Bernoulli number. The integral analog, also found by Ramanujan, is
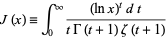 |
(7) |
(Berndt 1994, p. 129; Hardy 1999, p. 23).
REFERENCES:
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Borwein, J. M.; Bradley, D. M.; and Crandall, R. E. "Computational Strategies for the Riemann Zeta Function." J. Comput. Appl. Math. 121, 247-296, 2000.
Gram, J. P. "Undersøgelser angaaende Maengden af Primtal under en given Graeense." K. Videnskab. Selsk. Skr. 2, 183-308, 1884.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Ingham, A. E. Ch. 5 in The Distribution of Prime Numbers. New York: Cambridge University Press, 1990.
Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, p. 225, 1996.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 74, 1991.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|