Legendre Symbol

The Legendre symbol is a number theoretic function 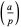 which is defined to be equal to  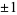depending on whether  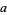is a quadratic residue modulo 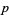. The definition is sometimes generalized to have value 0 if ,

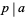(1)

If 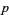 is an odd prime, then the Jacobi symbol reduces to the Legendre symbol. The Legendre symbol is implemented in the Wolfram Language via the Jacobi symbol, JacobiSymbol[a, p].

The Legendre symbol obeys the identity

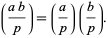(2)

Particular identities include

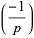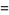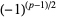			(3)
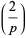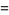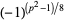			(4)
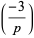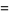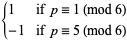			(5)
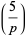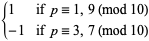			(6)

(Nagell 1951, p. 144), as well as the general

(7)

when 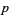 and 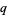 are both odd primes.

In general,

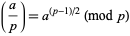(8)

if 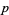 is an odd prime.

REFERENCES:

Guy, R. K. "Quadratic Residues. Schur's Conjecture." §F5 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 244-245, 1994.

Hardy, G. H. and Wright, E. M. "Quadratic Residues." §6.5 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 67-68, 1979.

Jones, G. A. and Jones, J. M. "The Legendre Symbol." §7.3 in Elementary Number Theory. Berlin: Springer-Verlag, pp. 123-129, 1998.

Nagell, T. "Euler's Criterion and Legendre's Symbol." §38 in Introduction to Number Theory. New York: Wiley, pp. 133-136, 1951.

Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 33-34 and 40-42, 1993.