


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-6-2020
Date: 12-1-2020
Date: 20-10-2019
|
A strong pseudoprime to a base 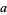 is an odd composite number
is an odd composite number 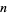 with
with 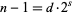 (for
(for 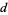 odd) for which either
odd) for which either
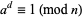 |
(1) |
or
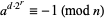 |
(2) |
for some 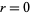 , 1, ...,
, 1, ..., 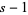 (Riesel 1994, p. 91). Note that Guy (1994, p. 27) restricts the definition of strong pseudoprimes to only those satisfying (1).
(Riesel 1994, p. 91). Note that Guy (1994, p. 27) restricts the definition of strong pseudoprimes to only those satisfying (1).
The definition is motivated by the fact that a Fermat pseudoprime 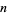 to the base
to the base 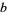 satisfies
satisfies
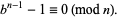 |
(3) |
But since 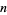 is odd, it can be written
is odd, it can be written 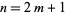 , and
, and
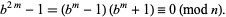 |
(4) |
If 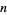 is prime, it must divide at least one of the factors, but can't divide both because it would then divide their difference
is prime, it must divide at least one of the factors, but can't divide both because it would then divide their difference
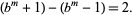 |
(5) |
Therefore,
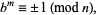 |
(6) |
so write 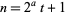 to obtain
to obtain
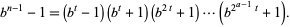 |
(7) |
If 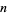 divides exactly one of these factors but is composite, it is a strong pseudoprime. A composite number is a strong pseudoprime to at most 1/4 of all bases less than itself (Monier 1980, Rabin 1980). The strong pseudoprimes provide the basis for Miller's primality test and Rabin-Miller strong pseudoprime test.
divides exactly one of these factors but is composite, it is a strong pseudoprime. A composite number is a strong pseudoprime to at most 1/4 of all bases less than itself (Monier 1980, Rabin 1980). The strong pseudoprimes provide the basis for Miller's primality test and Rabin-Miller strong pseudoprime test.
A strong pseudoprime to the base 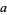 is also an Euler pseudoprime to the base
is also an Euler pseudoprime to the base 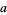 (Pomerance et al. 1980). The strong pseudoprimes include some Euler pseudoprimes, Fermat pseudoprimes, and Carmichael numbers.
(Pomerance et al. 1980). The strong pseudoprimes include some Euler pseudoprimes, Fermat pseudoprimes, and Carmichael numbers.
The following table lists the first few pseudoprimes to a number of small bases.
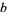 |
OEIS | 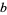 -strong pseudoprimes -strong pseudoprimes |
| 2 | A001262 | 2047, 3277, 4033, 4681, 8321, ... |
| 3 | A020229 | 121, 703, 1891, 3281, 8401, 8911, ... |
| 4 | A020230 | 341, 1387, 2047, 3277, 4033, 4371, ... |
| 5 | A020231 | 781, 1541, 5461, 5611, 7813, ... |
| 6 | A020232 | 217, 481, 1111, 1261, 2701, ... |
| 7 | A020233 | 25, 325, 703, 2101, 2353, 4525, ... |
| 8 | A020234 | 9, 65, 481, 511, 1417, 2047, ... |
| 9 | A020235 | 91, 121, 671, 703, 1541, 1729, ... |
The number of strong 2-pseudoprimes less than 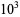 ,
, 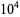 , ... are 0, 5, 16, 46, 162, ... (OEIS A055552). Note that Guy's (1994, p. 27) definition gives only the subset 2047, 4681, 15841, 42799, 52633, 90751, ..., giving counts inconsistent with those in Guy's table.
, ... are 0, 5, 16, 46, 162, ... (OEIS A055552). Note that Guy's (1994, p. 27) definition gives only the subset 2047, 4681, 15841, 42799, 52633, 90751, ..., giving counts inconsistent with those in Guy's table.
The strong 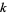 -pseudoprime test for
-pseudoprime test for 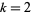 , 3, 5 correctly identifies all primes below
, 3, 5 correctly identifies all primes below 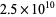 with only 13 exceptions, and if 7 is added, then the only exception less than
with only 13 exceptions, and if 7 is added, then the only exception less than 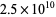 is 3215031751. Jaeschke (1993) showed that there are only 101 strong pseudoprimes for the bases 2, 3, and 5 less than
is 3215031751. Jaeschke (1993) showed that there are only 101 strong pseudoprimes for the bases 2, 3, and 5 less than 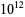 , nine if 7 is added, and none if 11 is added. Also, the bases 2, 13, 23, and 1662803 have no exceptions up to
, nine if 7 is added, and none if 11 is added. Also, the bases 2, 13, 23, and 1662803 have no exceptions up to 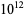 .
.
If 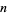 is composite, then there is a base for which
is composite, then there is a base for which 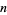 is not a strong pseudoprime. There are therefore no "strong Carmichael numbers." Let
is not a strong pseudoprime. There are therefore no "strong Carmichael numbers." Let 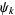 denote the smallest strong pseudoprime to all of the first
denote the smallest strong pseudoprime to all of the first 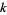 primes taken as bases (i.e., the smallest odd number for which the Rabin-Miller strong pseudoprime test on bases less than or equal to the
primes taken as bases (i.e., the smallest odd number for which the Rabin-Miller strong pseudoprime test on bases less than or equal to the 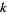 th prime
th prime 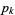 fails). Jaeschke (1993) computed
fails). Jaeschke (1993) computed 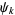 from
from 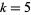 to 8 and gave upper bounds for
to 8 and gave upper bounds for 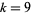 to 11.
to 11.
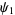 |
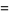 |
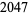 |
(8) |
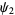 |
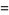 |
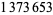 |
(9) |
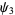 |
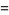 |
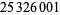 |
(10) |
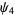 |
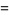 |
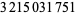 |
(11) |
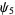 |
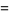 |
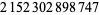 |
(12) |
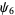 |
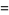 |
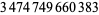 |
(13) |
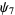 |
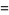 |
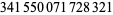 |
(14) |
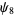 |
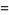 |
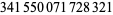 |
(15) |
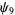 |
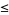 |
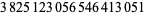 |
(16) |
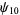 |
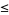 |
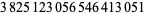 |
(17) |
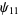 |
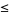 |
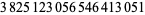 |
(18) |
(OEIS A014233), where the bounds for 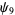 ,
, 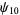 , and
, and 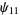 were determined by Zhang and Tang (2003). A seven-step test utilizing older bounds on these results (Riesel 1994) allows all numbers less than
were determined by Zhang and Tang (2003). A seven-step test utilizing older bounds on these results (Riesel 1994) allows all numbers less than 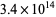 to be tested.
to be tested.
Zhang (2001, 2002, 2005, 2006, 2007) conjectured that
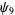 |
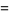 |
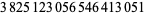 |
(19) |
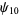 |
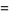 |
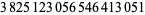 |
(20) |
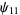 |
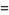 |
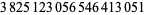 |
(21) |
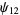 |
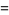 |
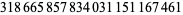 |
(22) |
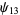 |
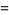 |
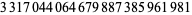 |
(23) |
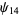 |
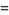 |
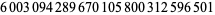 |
(24) |
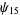 |
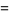 |
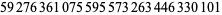 |
(25) |
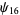 |
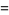 |
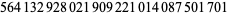 |
(26) |
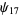 |
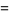 |
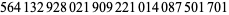 |
(27) |
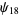 |
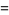 |
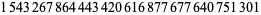 |
(28) |
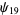 |
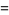 |
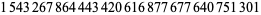 |
(29) |
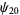 |
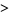 |
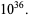 |
(30) |
The Baillie-PSW primality test is a test based on a combination of strong pseudoprimes and Lucas pseudoprimes proposed by Pomerance et al. (Pomerance et al. 1980, Pomerance 1984).
REFERENCES:
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, p. 57, 2007.
Baillie, R. and Wagstaff, S. "Lucas Pseudoprimes." Math. Comput. 35, 1391-1417, 1980. https://mpqs.free.fr/LucasPseudoprimes.pdf.
Guy, R. K. "Pseudoprimes. Euler Pseudoprimes. Strong Pseudoprimes." §A12 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 27-30, 1994.
Jaeschke, G. "On Strong Pseudoprimes to Several Bases." Math. Comput. 61, 915-926, 1993.
Monier, L. "Evaluation and Comparison of Two Efficient Probabilistic Primality Testing Algorithms." Theor. Comput. Sci. 12, 97-108, 1980.
Pinch, R. G. E. "The Pseudoprimes Up to 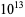 ." ftp://ftp.dpmms.cam.ac.uk/pub/PSP/.
." ftp://ftp.dpmms.cam.ac.uk/pub/PSP/.
Pomerance, C. "Are There Counterexamples to the Baillie-PSW Primality Test?" 1984. https://www.pseudoprime.com/dopo.pdf.
Pomerance, C.; Selfridge, J. L.; and Wagstaff, S. S. Jr. "The Pseudoprimes to 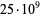 ." Math. Comput. 35, 1003-1026, 1980. https://mpqs.free.fr/ThePseudoprimesTo25e9.pdf.
." Math. Comput. 35, 1003-1026, 1980. https://mpqs.free.fr/ThePseudoprimesTo25e9.pdf.
Rabin, M. O. "Probabilistic Algorithm for Testing Primality." J. Number Th. 12, 128-138, 1980.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Basel: Birkhäuser, p. 92, 1994.
Sloane, N. J. A. Sequences A001262, A014233, A020229, A020230, A020231, A020232, A020233, A020234, A020235, A055552, and A102483 in "The On-Line Encyclopedia of Integer Sequences."
Zhang, Z. "Finding Strong Pseudoprimes to Several Bases." Math. Comput. 70, 863-872, 2001. https://www.ams.org/journal-getitem?pii=S0025-5718-00-01215-1.
Zhang, Z. "A One-Parameter Quadratic-Base Version of the Baillie-PSW Probable Prime Test." Math. Comput. 71, 1699-1734, 2002. https://www.ams.org/journal-getitem?pii=S0025-5718-02-01424-2.
Zhang, Z. "Finding 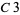 -Strong Pseudoprimes." Math. Comput. 74, 1009-1024, 2005. https://www.ams.org/mcom/2005-74-250/S0025-5718-04-01693-X/home.html.
-Strong Pseudoprimes." Math. Comput. 74, 1009-1024, 2005. https://www.ams.org/mcom/2005-74-250/S0025-5718-04-01693-X/home.html.
Zhang, Z. "Notes on Some New Kinds of Pseudoprimes." Math. Comput. 75, 451-460, 2006.
Zhang, Z. "Two Kinds of Strong Pseudoprimes up to 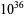 ." Math. Comput. 76, 2095-2107, 2007.
." Math. Comput. 76, 2095-2107, 2007.
Zhang, Z. and Tang, M. "Finding Strong Pseudoprimes to Several Bases, II." Math. Comput. 72, 2085-2097, 2003. https://www.ams.org/journal-getitem?pii=S0025-5718-03-01545-X.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|