


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-3-2020
Date: 7-11-2020
Date: 16-2-2020
|
Cube Line Picking--Face and Face
Instead of picking two points from the interior of the cube, instead pick two points on different faces of the unit cube. In this case, the average distance between the points is
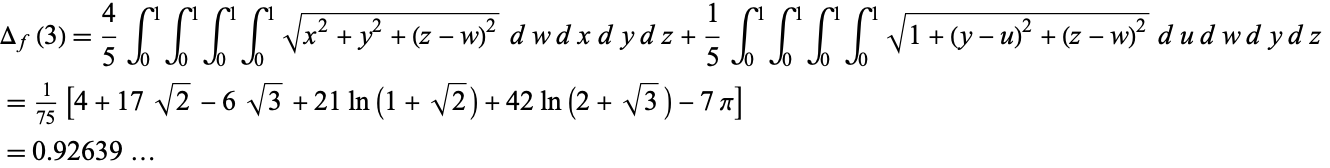 |
(1) |
(OEIS A093066; Borwein and Bailey 2003, p. 26; Borwein et al. 2004, pp. 66-67). Interestingly,
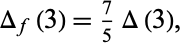 |
(2) |
as apparently first noted by M. Trott (pers. comm., Mar. 21, 2008).
The two integrals above can be written in terms of sums as
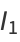 |
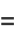 |
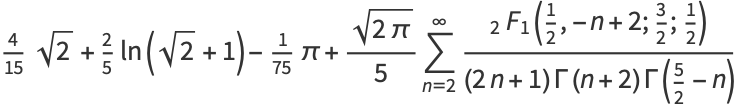 |
(3) |
 |
 |
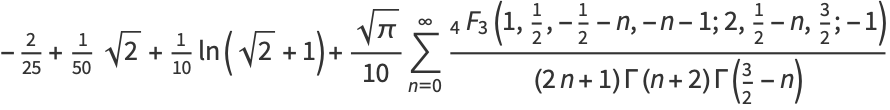 |
(4) |
(Borwein et al. 2004, p. 67), where however 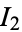 appears to be classically divergent and perhaps must be interpreted in some regularized sense.
appears to be classically divergent and perhaps must be interpreted in some regularized sense.
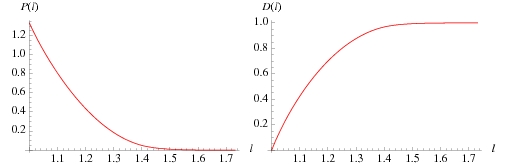
Consider a line whose endpoints are picked at random on opposite sides of the unit cube. The probability density function for the length 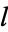 of this line is given by
of this line is given by
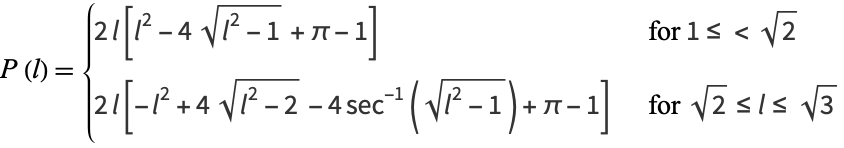 |
(5) |
(Mathai 1999; after simplification). The mean length is
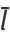 |
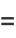 |
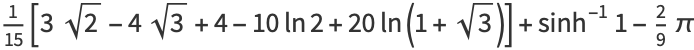 |
(6) |
 |
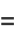 |
 |
(7) |
The first even raw moments 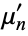 for
for 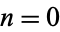 , 2, 4, ... are 1, 4/3, 167/90, 284/105, 931/225, 9868/1485, ....
, 2, 4, ... are 1, 4/3, 167/90, 284/105, 931/225, 9868/1485, ....
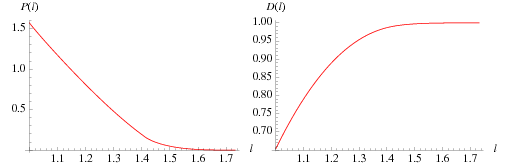
Consider a line whose endpoints are picked at random on adjacent sides of the unit cube. The probability density function for the length 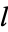 of this line is given by
of this line is given by
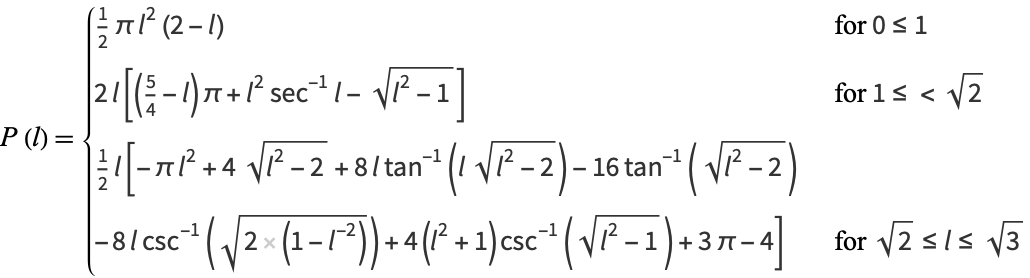 |
(8) |
(Mathai 1999; after simplification). The mean length is
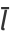 |
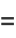 |
![1/(180)[42sqrt(2)-6sqrt(3)-11pi+504ln2-1008ln(1+sqrt(3))+600ln(2+sqrt(3))+18sinh^(-1)1]](http://mathworld.wolfram.com/images/equations/CubeLinePickingFaceandFace/Inline20.gif) |
(9) |
 |
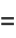 |
 |
(10) |
The first even raw moments 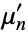 for
for 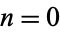 , 2, 4, ... are 1, 5/6, 41/45, 1469/1260, 5/3, 53947/20790, ....
, 2, 4, ... are 1, 5/6, 41/45, 1469/1260, 5/3, 53947/20790, ....
REFERENCES:
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Mathai, A. M.; Moschopoulos, P.; and Pederzoli, G. "Distance between Random Points in a Cube." J. Statistica 59, 61-81, 1999.
Sloane, N. J. A. Sequence A093066 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|