Circle Line Picking

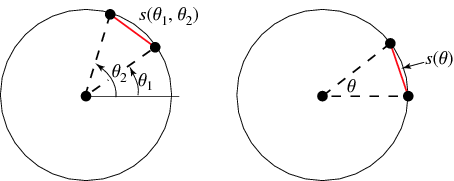
Given a unit circle, pick two points at random on its circumference, forming a chord. Without loss of generality, the first point can be taken as 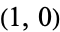, and the second by 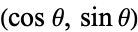, with  (by symmetry, the range can be limited to 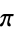 instead of 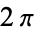). The distance  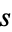between the two points is then

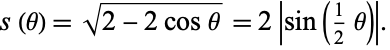(1)

The average distance is then given by

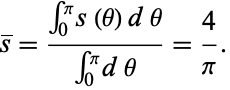(2)

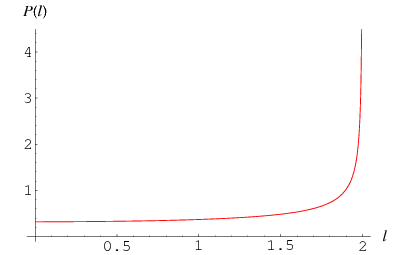
The probability density function 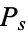 is obtained from

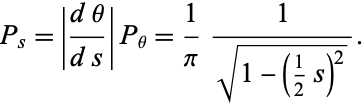(3)

The raw moments are then

			(4)
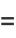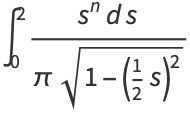			(5)
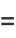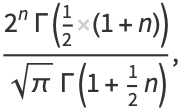			(6)

giving the first few as

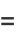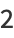			(7)
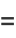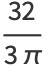			(8)
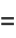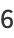			(9)
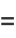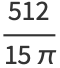			(10)
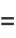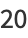			(11)

(OEIS A000984 and OEIS A093581 and A001803), where the numerators of the odd terms are 4 times OEIS A061549.

The central moments are

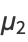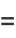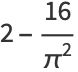			(12)
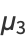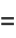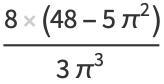			(13)
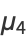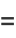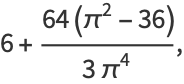			(14)

giving the skewness and kurtosis excess as

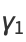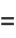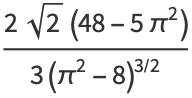			(15)
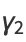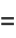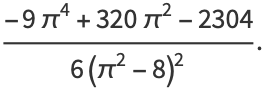			(16)

Bertrand's problem asks for the probability that a chord drawn at random on a circle of radius 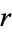 has length .

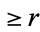REFERENCES:

Sloane, N. J. A. Sequences A000984/M1645, A001803/M2986, A061549, and A093581 in "The On-Line Encyclopedia of Integer Sequences."