


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-11-2019
Date: 26-8-2020
Date: 13-10-2020
|
The extension ring obtained from a commutative unit ring (other than the trivial ring) when allowing division by all non-zero divisors. The ring of fractions of an integral domain is always a field.
The term "ring of fractions" is sometimes used to denote any localization of a ring. The ring of fractions in the above meaning is then referred to as the total ring of fractions, and coincides with the localization with respect to the set of all non-zero divisors.
When defining addition and multiplication of fractions, all that is required of the denominators is that they be multiplicatively closed, i.e., if 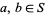 , then
, then 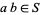 ,
,
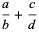 |
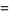 |
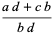 |
(1) |
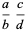 |
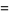 |
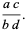 |
(2) |
Given a multiplicatively closed set 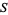 in a ring
in a ring 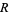 , the ring of fractions is all elements of the form
, the ring of fractions is all elements of the form 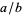 with
with 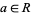 and
and 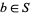 . Of course, it is required that
. Of course, it is required that 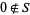 and that fractions of the form
and that fractions of the form 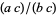 and
and 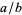 be considered equivalent. With the above definitions of addition and multiplication, this set forms a ring.
be considered equivalent. With the above definitions of addition and multiplication, this set forms a ring.
The original ring may not embed in this ring of fractions 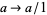 if it is not an integral domain. For instance, if
if it is not an integral domain. For instance, if 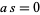 for some
for some 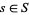 , then
, then 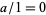 in the ring of fractions.
in the ring of fractions.
When the complement of 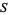 is an ideal
is an ideal 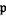 , it must be a prime ideal because
, it must be a prime ideal because 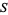 is multiplicatively closed. In this case, the ring of fractions is the localization at
is multiplicatively closed. In this case, the ring of fractions is the localization at 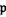 .
.
When the ring is an integral domain, then the nonzero elements are multiplicatively closed. Letting 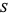 be the nonzero elements, then the ring of fractions is a field called the field of fractions, or the total ring of fractions. In this case one can also use the usual rule for division of fractions, which is not normally available for more general
be the nonzero elements, then the ring of fractions is a field called the field of fractions, or the total ring of fractions. In this case one can also use the usual rule for division of fractions, which is not normally available for more general 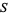 .
.
REFERENCES:
Atiyah, M. F. and Macdonald, I. G. Introduction to Commutative Algebra. Menlo Park, CA: Addison-Wesley, 1969.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|