Prime Difference Function

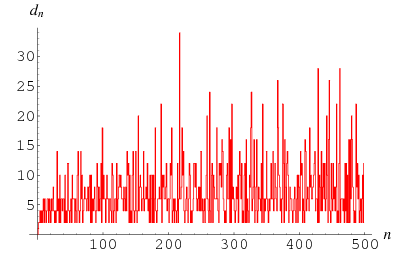
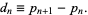(1)

The first few values are 1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, ... (OEIS A001223). Rankin has shown that

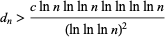(2)

for infinitely many 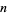 and for some constant  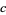(Guy 1994). At a March 2003 meeting on elementary and analytic number in Oberwolfach, Germany, Goldston and Yildirim presented an attempted proof that

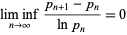(3)

(Montgomery 2003). Unfortunately, this proof turned out to be flawed.

An integer 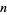 is called a jumping champion if  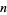is the most frequently occurring difference between consecutive primes  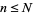for some  (Odlyzko et al.).

REFERENCES:

Bombieri, E. and Davenport, H. "Small Differences Between Prime Numbers." Proc. Roy. Soc. A 293, 1-18, 1966.

Erdős, P.; and Straus, E. G. "Remarks on the Differences Between Consecutive Primes." Elem. Math. 35, 115-118, 1980.

Guy, R. K. "Gaps between Primes. Twin Primes" and "Increasing and Decreasing Gaps." §A8 and A11 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 19-23 and 26-27, 1994.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 114-115, 2003.

Montgomery, H. "Small Gaps Between Primes." 13 Mar 2003. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0303&L=nmbrthry&P=1323.

Odlyzko, A.; Rubinstein, M.; and Wolf, M. "Jumping Champions." https://www.research.att.com/~amo/doc/recent.html.

Riesel, H. "Difference Between Consecutive Primes." Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, p. 9, 1994.

Sloane, N. J. A. Sequence A001223/M0296 in "The On-Line Encyclopedia of Integer Sequences."