


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-11-2019
Date: 6-10-2020
Date: 30-7-2020
|
A rational number expressed in the form 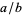 (in-line notation) or
(in-line notation) or 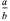 (traditional "display" notation), where
(traditional "display" notation), where 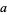 is called the numerator and
is called the numerator and 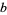 is called the denominator. When written in-line, the slash "/" between numerator and denominator is called a solidus.
is called the denominator. When written in-line, the slash "/" between numerator and denominator is called a solidus.
A mathematical joke states that 4/3 of people don't understand fractions.
A proper fraction is a fraction such that 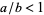 , and a reduced fraction is a fraction with common terms canceled out of the numerator and denominator.
, and a reduced fraction is a fraction with common terms canceled out of the numerator and denominator.
The Egyptians expressed their fractions as sums (and differences) of unit fractions. Conway and Guy (1996) give a table of Roman notation for fractions, in which multiples of 1/12 (the uncia) were given separate names.
The rules for the algebraic combination of fractions are given by
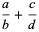 |
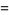 |
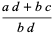 |
(1) |
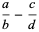 |
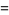 |
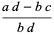 |
(2) |
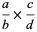 |
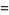 |
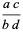 |
(3) |
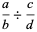 |
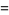 |
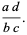 |
(4) |
Note however that the above results will not necessarily be reduced fractions.
REFERENCES:
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 22-23, 1996.
Courant, R. and Robbins, H. "Decimal Fractions. Infinite Decimals." §2.2.2 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 61-63, 1996.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|