المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | 600-Cell |
 1481
 01:50 صباحاً
date: 30-7-2020 |
Author : Coxeter, H. S. M 
Book or Source : Introduction to Geometry, 2nd ed. New York: Wiley, 1969. 
Page and Part : ...|
Read More
Date: 3-2-2021
1194
Date: 15-9-2020
1345
Date: 21-11-2019
875
|
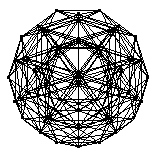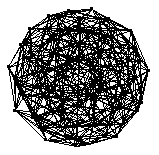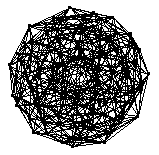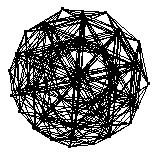
The 600-cell is the finite regular four-dimensional polytope with Schläfli symbol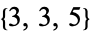 
. It is also known as the hypericosahedron or hexacosichoron. It is composed of 600 tetrahedra, with 5 to an edge. The 600-cell has 120 vertices (Coxeter 1969) and 720 edges. It is one of the six regular polychora.
In the plate following p. 160, Coxeter (1973) gives two illustrations of the polytope.
The dual of the 600-cell is the 120-cell.
The vertices of the 600-cell with circumradius 2 and edge length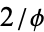 
, where 
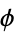is the golden ratio, are given by the following sets (Coxeter 1969, pp. 403-404).
1. The 96 even permutations of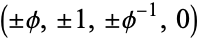 
.
2. The 8 permutations of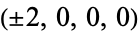 
.
3. The 16 permutations of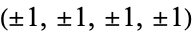 
.
There are 8 distinct nonzero distances between vertices of the 600-cell in 4-space.
The skeleton of the 600-cell, shown above in several projections, is a 12-regular graph of girth 3 and diameter 5. The numbers of vertices at graph distance 
, 1, 2, ... from a given vertex on the skeleton of the 600-cell are 1, 12, 32, 42, 32, and 1 (OEIS A118785). The graph spectrum of the 600-cell is ![12^1[3(1+/-sqrt(5))]^4[2(1+/-sqrt(5))]^9(+/-3)^(16)0^(25)(-2)^(36)](https://mathworld.wolfram.com/images/equations/600-Cell/Inline8.gif)
(Buekenhout and Parker 1998). The skeleton of the 600-cell is implemented in the Wolfram Language as GraphData["SixHundredCellGraph"].
The 600-cell has
 |
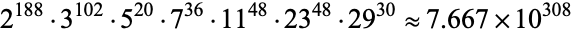distinct nets (Buekenhout and Parker 1998). The order of its automorphism group is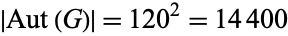 
(Buekenhout and Parker 1998).
The independence number of the 600-cell skeleton is 24 (Debroni et al. 2010) and its chromatic number is 5 (R. Pratt, pers. comm., Dec. 2, 2011).
REFERENCES:
Buekenhout, F. and Parker, M. "The Number of Nets of the Regular Convex Polytopes in Dimension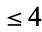 
." Disc. Math. 186, 69-94, 1998.
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, 1969.
Coxeter, H. S. M. "Gosset's Construction for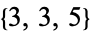 
. §8.5 in Regular Polytopes, 3rd ed. New York: Dover, pp. 136-137, 153-154, and 157, 1973.
Debroni, S.; Delisle, E.; Myrvold, W.; Sethi, A.; Whitney, J.; Woodcock, J.; Fowler, P. W.; de La La Vaissière, B.; and Deza, M. "Maximum Independent Sets of the 120-Cell and Other Regular Polyhedra." To appear in Ars Mathematica Contemporanea. 2010. https://www.liga.ens.fr/~deza/withFowler/120-cell_2010.pdf.
Sloane, N. J. A. Sequence A118785 in "The On-Line Encyclopedia of Integer Sequences."
Swab, E. "600-Cell." https://users.adelphia.net/~eswab/600cell.htm.
Weimholt, A. "600-Cell Foldout." https://www.weimholt.com/andrew/600.html.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 210, 1991.
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
