Zonal Harmonic

A zonal harmonic is a spherical harmonic of the form 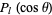, i.e., one which reduces to a Legendre polynomial (Whittaker and Watson 1990, p. 302). These harmonics are termed "zonal" since the curves on a unit sphere (with center at the origin) on which  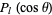vanishes are  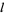parallels of latitude which divide the surface into zones (Whittaker and Watson 1990, p. 392).

Resolving 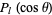 into factors linear in 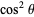, multiplied by  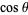when 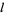 is odd, then replacing  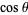by 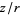 allows the zonal harmonic  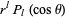to be expressed as a product of factors linear in 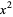, , 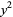and 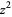, with the product multiplied by  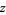when 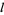 is odd (Whittaker and Watson 1990, p. 1990).

REFERENCES:

Byerly, W. E. "Zonal Harmonics." Ch. 5 in An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, pp. 144-194, 1959.

Hashiguchi, H. and Niki, N. "Algebraic Algorithm for Calculating Coefficients of Zonal Polynomials of Order Three." J. Japan. Soc. Comput. Statist. 10, 41-46, 1997.

Kowata, A. and Wada, R. "Zonal Polynomials on the Space of 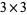 Positive Definite Symmetric Matrices." Hiroshima Math. J. 22, 433-443, 1992.

Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.