


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-5-2019
Date: 25-4-2019
Date: 13-6-2019
|
Although Bessel functions of the second kind are sometimes called Weber functions, Abramowitz and Stegun (1972) define a separate Weber function as
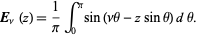 |
(1) |
These function may also be written as
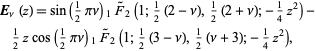 |
(2) |
where 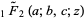 is a regularized hypergeometric function.
is a regularized hypergeometric function.
This function is implemented in the Wolfram Language as WeberE[nu, z] and is an analog of the Anger function.
Special values for real  include
include
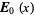 |
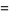 |
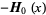 |
(3) |
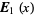 |
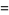 |
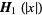 |
(4) |
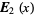 |
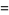 |
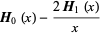 |
(5) |
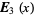 |
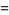 |
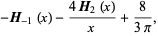 |
(6) |
where 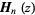 is a Struve function.
is a Struve function.
Letting 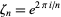 be a root of unity, another set of Weber functions is defined as
be a root of unity, another set of Weber functions is defined as
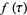 |
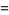 |
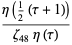 |
(7) |
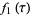 |
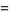 |
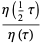 |
(8) |
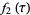 |
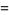 |
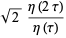 |
(9) |
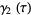 |
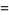 |
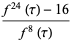 |
(10) |
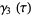 |
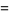 |
![([f^(24)(tau)+8][f_1^8(tau)-f_2^8(tau)])/(f^8(tau))](http://mathworld.wolfram.com/images/equations/WeberFunctions/Inline31.gif) |
(11) |
(Weber 1902, Atkin and Morain 1993), where 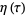 is the Dedekind eta function and
is the Dedekind eta function and  is the half-period ratio. These functions are related to the Ramanujan g- and G-functions and the elliptic lambda function.
is the half-period ratio. These functions are related to the Ramanujan g- and G-functions and the elliptic lambda function.
The Weber functions satisfy the identities
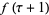 |
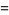 |
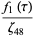 |
(12) |
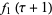 |
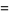 |
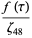 |
(13) |
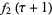 |
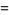 |
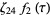 |
(14) |
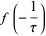 |
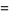 |
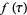 |
(15) |
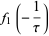 |
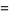 |
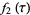 |
(16) |
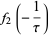 |
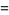 |
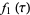 |
(17) |
(Weber 1902, Atkin and Morain 1993).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Anger and Weber Functions." §12.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 498-499, 1972.
Atkin, A. O. L. and Morain, F. "Elliptic Curves and Primality Proving." Math. Comput. 61, 29-68, 1993.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 68-69, 1987.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Anger Function 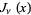 and Weber Function
and Weber Function 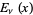 ." §1.5 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, p. 28, 1990.
." §1.5 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, p. 28, 1990.
Weber, H. Lehrbuch der Algebra, Vols. I-II. New York: Chelsea, pp. 113-114, 1902.
Weng, A. "Class Polynomials of CM-Fields. http://www.exp-math.uni-essen.de/zahlentheorie/classpol/class.html.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|