

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Elliptic Integral
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
"Elliptic Integrals." Ch. 17 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
25-4-2019
3482
Elliptic Integral
An elliptic integral is an integral of the form
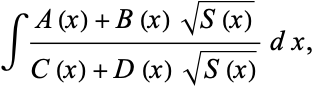 |
(1) |
or
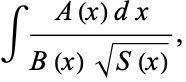 |
(2) |
where 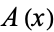 ,
, 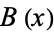 ,
, 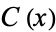 , and
, and 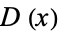 are polynomials in
are polynomials in 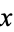 , and
, and 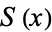 is a polynomial of degree 3 or 4. Stated more simply, an elliptic integral is an integral of the form
is a polynomial of degree 3 or 4. Stated more simply, an elliptic integral is an integral of the form
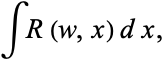 |
(3) |
where 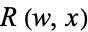 is a rational function of
is a rational function of 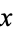 and
and 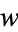 ,
, 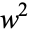 is a function of
is a function of 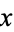 that is cubic or quartic in
that is cubic or quartic in 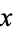 ,
, 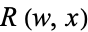 contains at least one odd power of
contains at least one odd power of 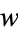 , and
, and 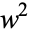 has no repeated factors (Abramowitz and Stegun 1972, p. 589).
has no repeated factors (Abramowitz and Stegun 1972, p. 589).
Elliptic integrals can be viewed as generalizations of the inverse trigonometric functions and provide solutions to a wider class of problems. For instance, while the arc length of a circle is given as a simple function of the parameter, computing the arc length of an ellipse requires an elliptic integral. Similarly, the position of a pendulum is given by a trigonometric function as a function of time for small angle oscillations, but the full solution for arbitrarily large displacements requires the use of elliptic integrals. Many other problems in electromagnetism and gravitation are solved by elliptic integrals.
A very useful class of functions known as elliptic functions is obtained by inverting elliptic integrals to obtain generalizations of the trigonometric functions. Elliptic functions (among which the Jacobi elliptic functions and Weierstrass elliptic function are the two most common forms) provide a powerful tool for analyzing many deep problems in number theory, as well as other areas of mathematics.
All elliptic integrals can be written in terms of three "standard" types. To see this, write
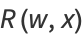 |
 |
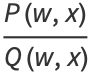 |
(4) |
 |
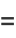 |
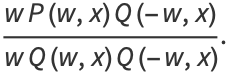 |
(5) |
But since 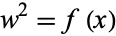 ,
,
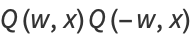 |
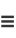 |
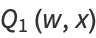 |
(6) |
 |
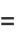 |
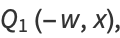 |
(7) |
then
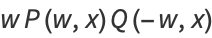 |
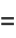 |
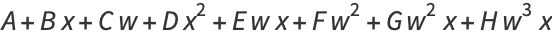 |
(8) |
 |
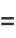 |
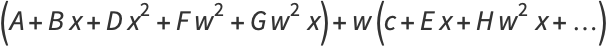 |
(9) |
 |
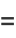 |
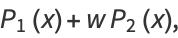 |
(10) |
so
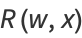 |
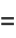 |
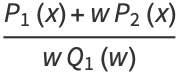 |
(11) |
 |
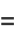 |
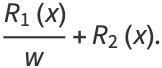 |
(12) |
But any function 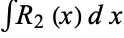 can be evaluated in terms of elementary functions, so the only portion that need be considered is
can be evaluated in terms of elementary functions, so the only portion that need be considered is
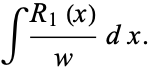 |
(13) |
Now, any quartic can be expressed as 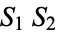 where
where
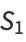 |
 |
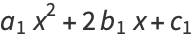 |
(14) |
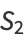 |
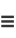 |
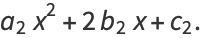 |
(15) |
The coefficients here are real, since pairs of complex roots are complex conjugates
![[x-(R+Ii)][x-(R-Ii)]](http://mathworld.wolfram.com/images/equations/EllipticIntegral/Inline52.gif) |
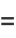 |
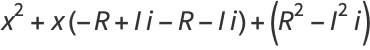 |
(16) |
 |
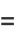 |
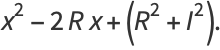 |
(17) |
If all four roots are real, they must be arranged so as not to interleave (Whittaker and Watson 1990, p. 514). Now define a quantity 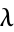 such that
such that 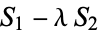
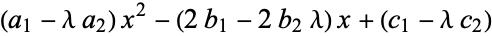 |
(18) |
is a square number and
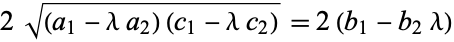 |
(19) |
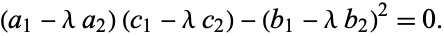 |
(20) |
Call the roots of this equation 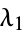 and
and 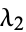 , then
, then
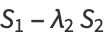 |
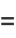 |
![[sqrt((a_1-lambda_2a_2)x^2)+sqrt(c_1-lambda_2c_2)]^2](http://mathworld.wolfram.com/images/equations/EllipticIntegral/Inline64.gif) |
(21) |
 |
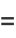 |
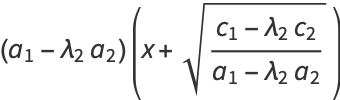 |
(22) |
 |
 |
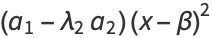 |
(23) |
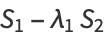 |
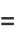 |
![[sqrt((a_1-lambda_1a_2)x^2)+sqrt(c_1-lambda_1c_2)]^2](http://mathworld.wolfram.com/images/equations/EllipticIntegral/Inline73.gif) |
(24) |
 |
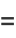 |
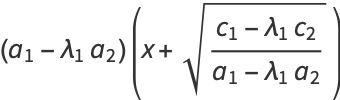 |
(25) |
 |
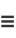 |
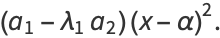 |
(26) |
Taking (25)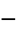 (26) and
(26) and 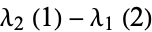 gives
gives
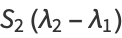 |
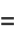 |
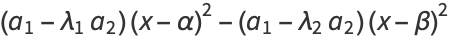 |
(27) |
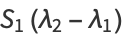 |
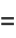 |
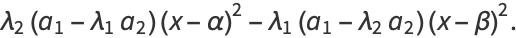 |
(28) |
Solving gives
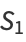 |
 |
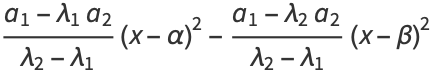 |
(29) |
 |
 |
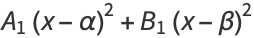 |
(30) |
 |
 |
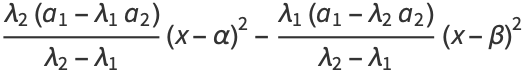 |
(31) |
 |
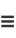 |
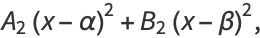 |
(32) |
so we have
![w^2=S_1S_2=[A_1(x-alpha)^2+B_1(x-beta)^2][A^2(x-alpha)^2+B^2(x-beta)^2].](http://mathworld.wolfram.com/images/equations/EllipticIntegral/NumberedEquation8.gif) |
(33) |
Now let
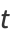 |
 |
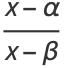 |
(34) |
 |
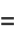 |
![[(x-beta)^(-1)-(x-alpha)(x-beta)^(-2)]dx](http://mathworld.wolfram.com/images/equations/EllipticIntegral/Inline105.gif) |
(35) |
 |
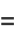 |
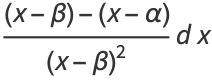 |
(36) |
 |
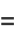 |
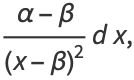 |
(37) |
so
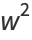 |
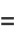 |
![(x-beta)^4[A_1((x-alpha)/(x-beta))^2+B_1][A_2((x-alpha)/(x-beta))+B_2]](http://mathworld.wolfram.com/images/equations/EllipticIntegral/Inline114.gif) |
(38) |
 |
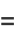 |
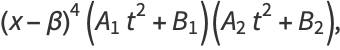 |
(39) |
and
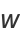 |
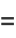 |
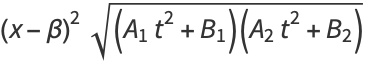 |
(40) |
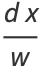 |
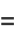 |
![[((x-beta)^2)/(alpha-beta)dt]1/((x-beta)^2sqrt((A_1t^2+B_1)(A_2t^2+B_2)))](http://mathworld.wolfram.com/images/equations/EllipticIntegral/Inline123.gif) |
(41) |
 |
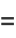 |
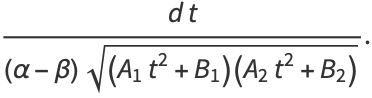 |
(42) |
Now let
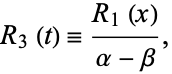 |
(43) |
so
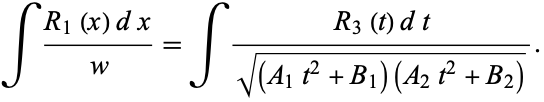 |
(44) |
Rewriting the even and odd parts
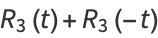 |
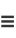 |
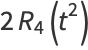 |
(45) |
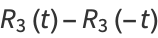 |
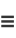 |
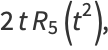 |
(46) |
gives
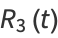 |
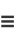 |
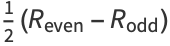 |
(47) |
 |
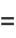 |
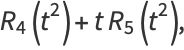 |
(48) |
so we have
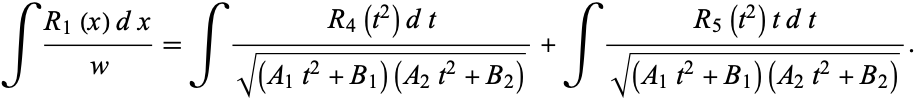 |
(49) |
Letting
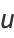 |
 |
 |
(50) |
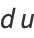 |
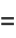 |
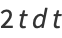 |
(51) |
reduces the second integral to
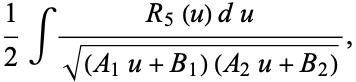 |
(52) |
which can be evaluated using elementary functions. The first integral can then be reduced by integration by parts to one of the three Legendre elliptic integrals (also called Legendre-Jacobi elliptic integrals), known as incomplete elliptic integrals of the first, second, and third kinds, denoted 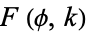 ,
, 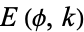 , and
, and 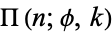 , respectively (von Kármán and Biot 1940, Whittaker and Watson 1990, p. 515). If
, respectively (von Kármán and Biot 1940, Whittaker and Watson 1990, p. 515). If 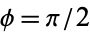 , then the integrals are called complete elliptic integrals and are denoted
, then the integrals are called complete elliptic integrals and are denoted 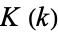 ,
, 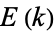 ,
, 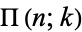 .
.
Incomplete elliptic integrals are denoted using a elliptic modulus 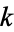 , parameter
, parameter 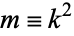 , or modular angle
, or modular angle 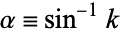 . An elliptic integral is written
. An elliptic integral is written 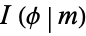 when the parameter is used,
when the parameter is used, 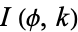 when the elliptic modulus is used, and
when the elliptic modulus is used, and 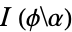 when the modular angle is used. Complete elliptic integrals are defined when
when the modular angle is used. Complete elliptic integrals are defined when 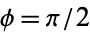 and can be expressed using the expansion
and can be expressed using the expansion
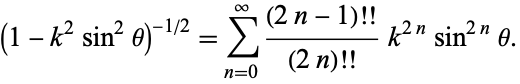 |
(53) |
An elliptic integral in standard form
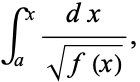 |
(54) |
where
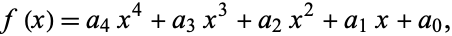 |
(55) |
can be computed analytically (Whittaker and Watson 1990, p. 453) in terms of the Weierstrass elliptic function with invariants
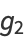 |
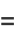 |
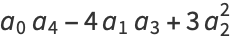 |
(56) |
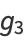 |
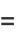 |
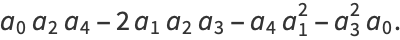 |
(57) |
If 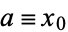 is a root of
is a root of 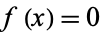 , then the solution is
, then the solution is
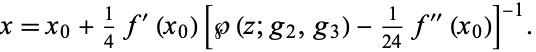 |
(58) |
For an arbitrary lower bound,
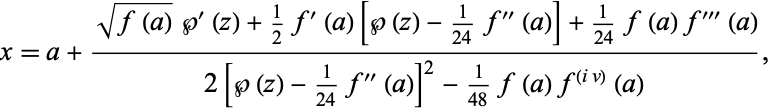 |
(59) |
where 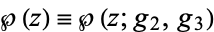 is a Weierstrass elliptic function (Whittaker and Watson 1990, p. 454).
is a Weierstrass elliptic function (Whittaker and Watson 1990, p. 454).
A generalized elliptic integral can be defined by the function
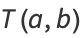 |
 |
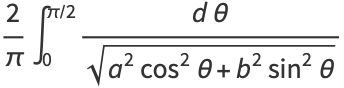 |
(60) |
 |
 |
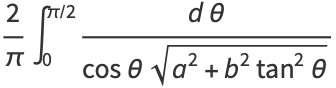 |
(61) |
(Borwein and Borwein 1987). Now let
 |
 |
 |
(62) |
 |
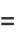 |
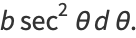 |
(63) |
But
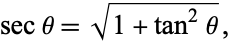 |
(64) |
so
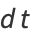 |
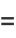 |
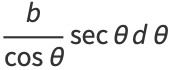 |
(65) |
 |
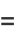 |
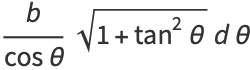 |
(66) |
 |
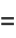 |
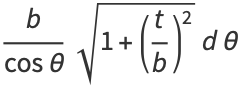 |
(67) |
 |
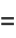 |
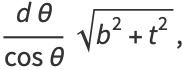 |
(68) |
and
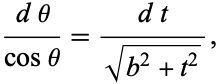 |
(69) |
and the equation becomes
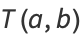 |
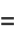 |
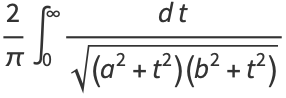 |
(70) |
 |
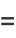 |
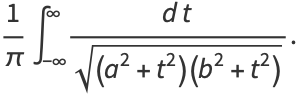 |
(71) |
Now we make the further substitution 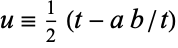 . The differential becomes
. The differential becomes
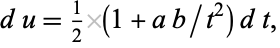 |
(72) |
but 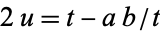 , so
, so
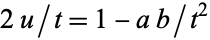 |
(73) |
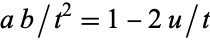 |
(74) |
and
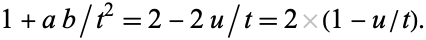 |
(75) |
However, the left side is always positive, so
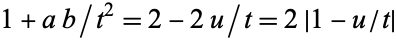 |
(76) |
and the differential is
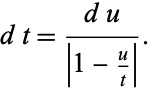 |
(77) |
We need to take some care with the limits of integration. Write (◇) as
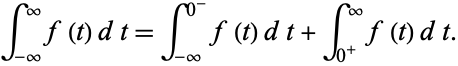 |
(78) |
Now change the limits to those appropriate for the 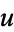 integration
integration
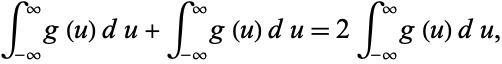 |
(79) |
so we have picked up a factor of 2 which must be included. Using this fact and plugging (◇) in (◇) therefore gives
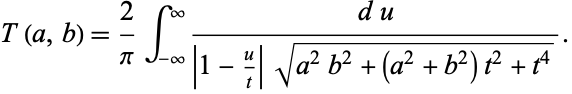 |
(80) |
Now note that
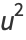 |
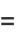 |
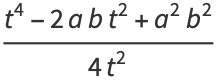 |
(81) |
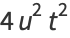 |
 |
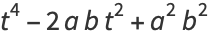 |
(82) |
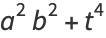 |
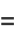 |
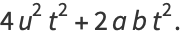 |
(83) |
Plug (◇) into (◇) to obtain
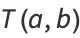 |
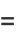 |
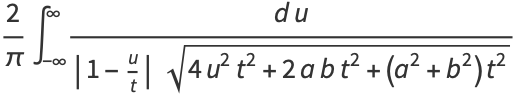 |
(84) |
 |
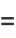 |
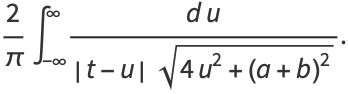 |
(85) |
But
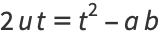 |
(86) |
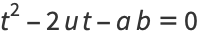 |
(87) |
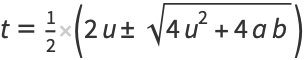 |
(88) |
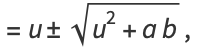 |
(89) |
so
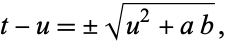 |
(90) |
and (◇) becomes
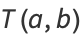 |
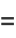 |
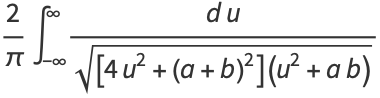 |
(91) |
 |
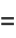 |
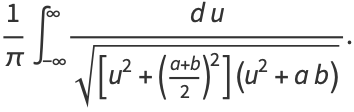 |
(92) |
We have therefore demonstrated that
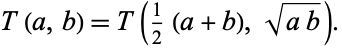 |
(93) |
We can thus iterate
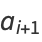 |
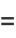 |
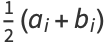 |
(94) |
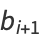 |
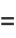 |
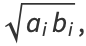 |
(95) |
as many times as we wish, without changing the value of the integral. But this iteration is the same as and therefore converges to the arithmetic-geometric mean, so the iteration terminates at 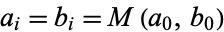 , and we have
, and we have
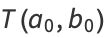 |
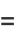 |
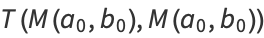 |
(96) |
 |
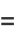 |
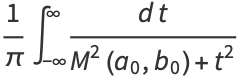 |
(97) |
 |
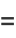 |
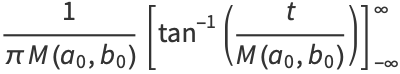 |
(98) |
 |
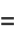 |
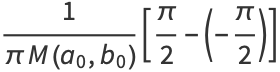 |
(99) |
 |
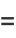 |
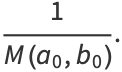 |
(100) |
Complete elliptic integrals arise in finding the arc length of an ellipse and the period of a pendulum. They also arise in a natural way from the theory of theta functions. Complete elliptic integrals can be computed using a procedure involving the arithmetic-geometric mean. Note that
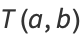 |
 |
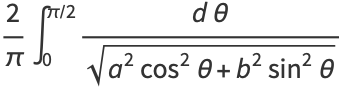 |
(101) |
 |
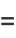 |
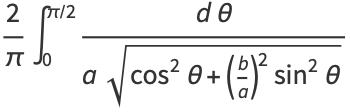 |
(102) |
 |
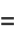 |
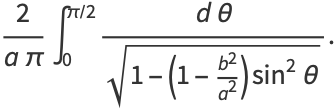 |
(103) |
So we have
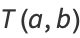 |
 |
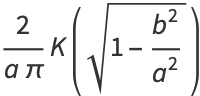 |
(104) |
 |
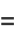 |
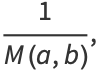 |
(105) |
where 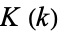 is the complete elliptic integral of the first kind. We are free to let
is the complete elliptic integral of the first kind. We are free to let 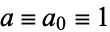 and
and 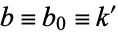 , so
, so
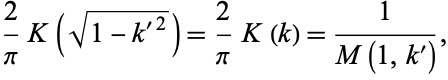 |
(106) |
since 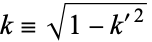 , so
, so
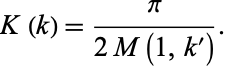 |
(107) |
But the arithmetic-geometric mean is defined by
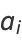 |
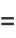 |
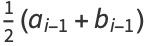 |
(108) |
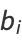 |
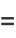 |
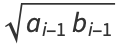 |
(109) |
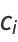 |
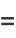 |
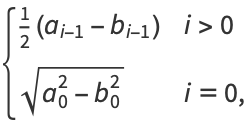 |
(110) |
where
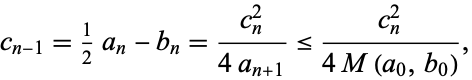 |
(111) |
so we have
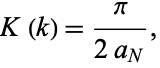 |
(112) |
where 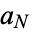 is the value to which
is the value to which 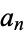 converges. Similarly, taking instead
converges. Similarly, taking instead 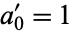 and
and 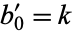 gives
gives
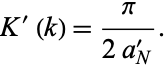 |
(113) |
Borwein and Borwein (1987) also show that defining
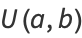 |
 |
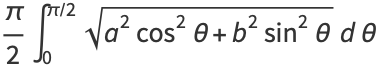 |
(114) |
 |
 |
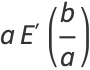 |
(115) |
leads to
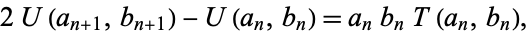 |
(116) |
so
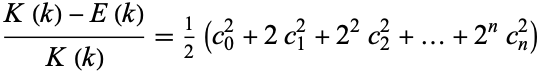 |
(117) |
for 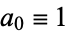 and
and 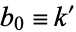 , and
, and
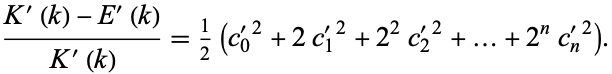 |
(118) |
The elliptic integrals satisfy a large number of identities. The complementary functions and moduli are defined by
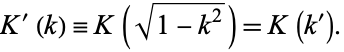 |
(119) |
Use the identity of generalized elliptic integrals
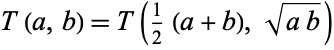 |
(120) |
to write
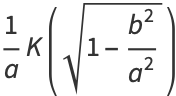 |
 |
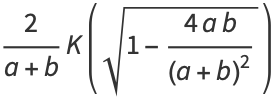 |
(121) |
 |
 |
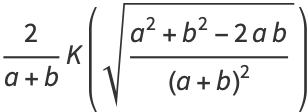 |
(122) |
 |
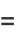 |
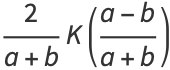 |
(123) |
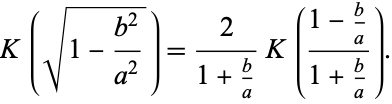 |
(124) |
Define
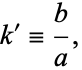 |
(125) |
and use
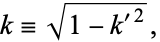 |
(126) |
so
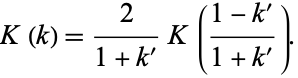 |
(127) |
Now letting 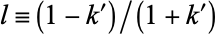 gives
gives
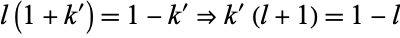 |
(128) |
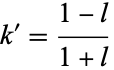 |
(129) |
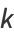 |
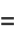 |
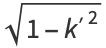 |
(130) |
 |
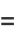 |
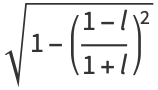 |
(131) |
 |
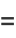 |
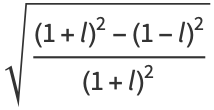 |
(132) |
 |
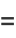 |
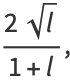 |
(133) |
and
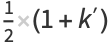 |
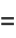 |
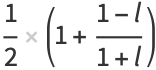 |
(134) |
 |
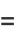 |
![1/2[((1+l)+(1-l))/(1+l)]](http://mathworld.wolfram.com/images/equations/EllipticIntegral/Inline315.gif) |
(135) |
 |
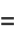 |
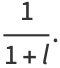 |
(136) |
Writing 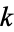 instead of
instead of 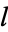 ,
,
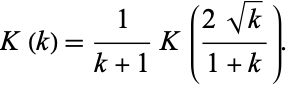 |
(137) |
Similarly, from Borwein and Borwein (1987),
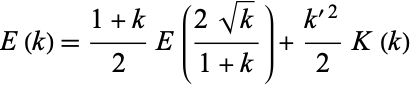 |
(138) |
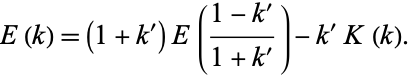 |
(139) |
Expressions in terms of the complementary function can be derived from interchanging the moduli and their complements in (◇), (◇), (◇), and (◇).
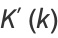 |
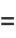 |
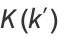 |
(140) |
 |
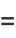 |
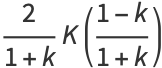 |
(141) |
 |
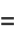 |
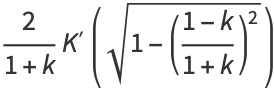 |
(142) |
 |
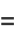 |
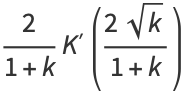 |
(143) |
 |
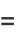 |
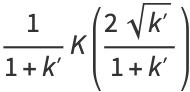 |
(144) |
 |
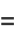 |
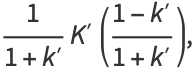 |
(145) |
and
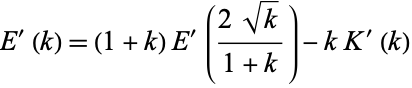 |
(146) |
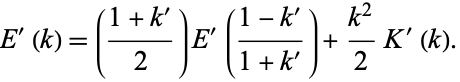 |
(147) |
Taking the ratios
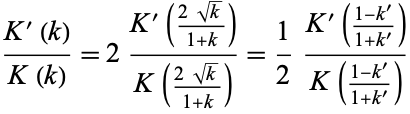 |
(148) |
gives the modular equation of degree 2. It is also true that
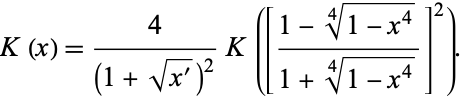 |
(149) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Elliptic Integrals." Ch. 17 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 587-607, 1972.
Arfken, G. "Elliptic Integrals." §5.8 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 321-327, 1985.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Hancock, H. Elliptic Integrals. New York: Wiley, 1917.
Kármán, T. von and Biot, M. A. Mathematical Methods in Engineering: An Introduction to the Mathematical Treatment of Engineering Problems. New York: McGraw-Hill, p. 121, 1940.
King, L. V. The Direct Numerical Calculation of Elliptic Functions and Integrals. London: Cambridge University Press, 1924.
PaliMathov, V. and Solovyev, Y. Elliptic Functions and Elliptic Integrals. Providence, RI: Amer. Math. Soc., 1997.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Elliptic Integrals and Jacobi Elliptic Functions." §6.11 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 254-263, 1992.
Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. Integrals and Series, Vol. 1: Elementary Functions. New York: Gordon & Breach, 1986.
Timofeev, A. F. Integration of Functions. Moscow and Leningrad: GTTI, 1948.
Weisstein, E. W. "Books about Elliptic Integrals." http://www.ericweisstein.com/encyclopedias/books/EllipticIntegrals.html.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Woods, F. S. "Elliptic Integrals." Ch. 16 in Advanced Calculus: A Course Arranged with Special Reference to the Needs of Students of Applied Mathematics. Boston, MA: Ginn, pp. 365-386, 1926.
 الاكثر قراءة في التفاضل و التكامل
الاكثر قراءة في التفاضل و التكامل
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















