


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-6-2019
Date: 23-4-2019
Date: 22-8-2019
|
There are several functions called "Lommel functions." One type of Lommel function appear in the solution to the Lommel differential equation and are given by
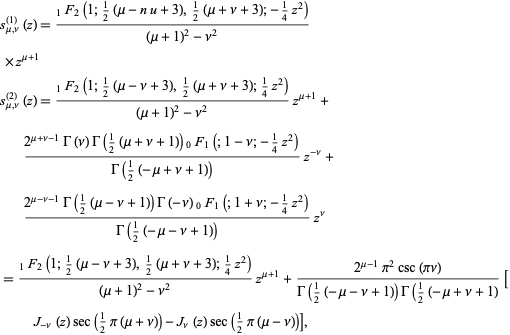 |
(1) |
where 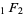 and
and 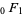 are generalized and confluence hypergeometric functions, respectively and
are generalized and confluence hypergeometric functions, respectively and 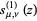 is typically denoted just as
is typically denoted just as 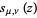 .
.
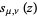 is also given by
is also given by
![s_(mu,nu)(z)=1/2pi[Y_nu(z)int_0^zz^muJ_nu(z)dz-J_nu(z)int_0^zz^muY_nu(z)dz],](http://mathworld.wolfram.com/images/equations/LommelFunction/NumberedEquation2.gif) |
(2) |
where 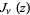 and
and 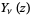 are Bessel functions of the first and second kinds (Watson 1966, p. 346; Gradshteyn and Ryzhik 2000, pp. 936-937).
are Bessel functions of the first and second kinds (Watson 1966, p. 346; Gradshteyn and Ryzhik 2000, pp. 936-937).
If a minus sign precedes the 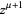 term in the general form of Lommel differential equation, then the solution is
term in the general form of Lommel differential equation, then the solution is
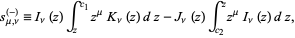 |
(3) |
where 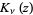 and
and 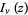 are modified Bessel functions of the first and second kinds.
are modified Bessel functions of the first and second kinds.
A function 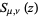 closely related to
closely related to 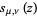 is also sometimes defined (Gradshteyn and Ryzhik 2000, p. 936).
is also sometimes defined (Gradshteyn and Ryzhik 2000, p. 936).
Lommel functions of two variables are related to the Bessel function of the first kind and arise in the theory of diffraction (Chandrasekhar 1960, p. 369) and, in particular, Mie scattering (Watson 1966, p. 537),
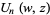 |
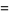 |
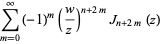 |
(4) |
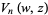 |
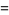 |
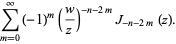 |
(5) |
These functions were first defined by Lommel (1884-1886ab). Note that the definition (5) of 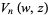 differs by a factor of
differs by a factor of 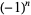 from the modern convention (Watson 1966, p. 537) and from the definition of Born and Wolf (1989, p. 438).
from the modern convention (Watson 1966, p. 537) and from the definition of Born and Wolf (1989, p. 438).
REFERENCES:
Born, M. and Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference, and Diffraction of Light, 6th ed.New York: Pergamon Press, 1989.
Chandrasekhar, S. Radiative Transfer. New York: Dover, p. 369, 1960.
Gilbert, L. P. "Recherches analytiques sur la diffraction de la lumière." Mém. courmonnées de l'Acad. R. des Sci. de Bruxelles 31, 1-52, 1863.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, pp. 936-937, 2000.
Gray, A. and Mathews, G. B. Ch. 14 in A Treatise on Bessel Functions and Their Applications to Physics, 2nd ed. New York: Dover, 1966.
Hardy, G. H. "General Theorems in Contour Integration with Some Applications." Quart. J. 32, 369-384, 1901.
Hardy, G. H. "On Certain Definite INtegrals Whose Values Can be Expressed in Terms of Bessel's Functions." Messenger Math.38, 129-132, 1909.
Lommel, E. C. J. von. "Die Beugungserscheinungen einer kreisrunden Oeffnung und eines kreisrunden Schirmchens theoretisch und experimentell bearbeitet." Abh. der math. phys. Classe der k. b. Akad. der Wiss. (München) 15, 229-328, 1884-1886a.
Lommel, E. C. J. von. "Die Beugungserscheinungen geradlinig begrenzter Schirme." Abh. der math. phys. Classe der k. b. Akad. der Wiss. (München) 15, 529-664, 1884-1886b.
Mayall, R. H. D. "On the Diffraction Pattern near the Focus of a Telescope." Proc. Cambridge Philos. Soc. 9, 259-269, 1898.
Pocklington, H. C. "Growth of a Wave-Group When the Group-Velocity Is Negative." Nature 71, 607-608, 1905.
Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Lommel Functions 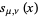 and
and 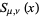 ." §1.5 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 28-29, 1990.
." §1.5 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 28-29, 1990.
Schafheitlin, F. "Beziehungen zwischen dem Integrallogarithmus und den Besselschen Funktionen." Berliner Sitzungsber. 8, 62-67, 1909.
Walker, J. The Analytical Theory of Light. London: Cambridge University Press, p. 396, 1904.
Watson, G. N. §16.5-16.59 in A Treatise on the Theory of Bessel Functions, 2nd ed. Cambridge, England: Cambridge University Press, pp. 537-550, 1966.



|
|
|
|
ما أبرز التغيرات التي تحدث عند الرجال عندما يصبحون آباءً؟
|
|
|
|
|
|
|
حقائق مثيرة للاهتمام حول الأرض
|
|
|
|
|
|
|
المجمع العلمي يحتفي بذكرى عيد الغدير في بغداد
|
|
|