Dyson Mod 27 Identities

The Dyson mod 27 identities are a set of four Rogers-Ramanujan-like identities given by

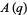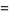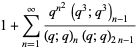			(1)
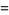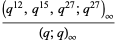			(2)
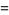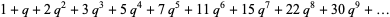			(3)
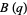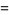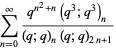			(4)
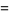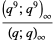			(5)
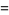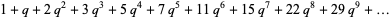			(6)
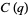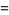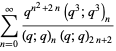			(7)
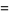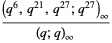			(8)
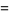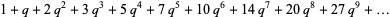			(9)
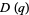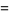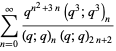			(10)
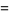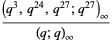			(11)
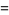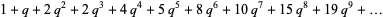			(12)

(OEIS A104501, A104502, A104503, and A104504).

Bailey (1947) systematically studied and generalized Rogers's work on Rogers-Ramanujan type identities in a paper submitted in late 1943. At the time, G. H. Hardy was the editor of the Proceedings of the London Mathematical Society and Hardy had recently taught the young Freeman Dyson in one of his undergraduate classes at Cambridge. He was therefore aware of Dyson's interest in Ramanujan-Rogers-type identities through his rediscovery of the Rogers-Selberg identities. Ignoring the usual convention of keeping the referee anonymous (since as far as Hardy knew, Bailey and Dyson were the only two people in all of England who were interested in Rogers-Ramanujan type identities at the time) and thinking that they would like to be in contact with each other), Hardy asked Dyson to referee Bailey's paper.

A correspondence between Bailey and Dyson ensued. Using the ideas in Bailey's paper, Dyson discovered a number of new Rogers-Ramanujan-type identities, including the four mod 27 identities above. Bailey suggested that Dyson publish his results in a separate paper, but Dyson declined, instead asking Bailey to include these identities in his own paper (with proper attribution to Dyson of course), which is what was done.

Due to the paper shortage caused by World War II, Bailey's paper wasn't published until 1947. Bailey's followup paper (Bailey 1949) was submitted about six months later and once again Dyson refereed it as well as contributed some additional identities.

REFERENCES:

Bailey, W. N. "Some Identities in Combinatory Analysis." Proc. London Math. Soc. 49, 421-435, 1947.

Bailey, W. N, "Identities of the Rogers-Ramanujan type." Proc. London Math. Soc., 50, 421-435, 1949.

Mc Laughlin, J.; Sills, A. V.; and Zimmer, P. "Dynamic Survey DS15: Rogers-Ramanujan-Slater Type Identities." Electronic J. Combinatorics, DS15, 1-59, May 31, 2008. http://www.combinatorics.org/Surveys/ds15.pdf.