


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 2-2-2017
Date: 26-1-2017
Date: 26-1-2017
|
Information Conservation
In both classical and quantum mechanics there is a very precise sense in which information is never lost from a closed isolated system. In classical physics the principle is embodied in Liouville's theorem: the conservation of phase space volume. If we begin following a system with some limited knowledge of its exact state, we might represent this by specifying an initial region Γ(0) in the system's phase space. The region Γ(0) has a volume VΓ in the phase space.
Now we let the system evolve. The region Γ(0) = Γ evolves into the region Γ(t). Liouville's theorem tells us that the volume of Γ(t) is exactly the same as that of Γ. In this sense the amount of information is conserved.
In a practical sense, information is lost because for most cases of interest the region Γ becomes very complicated like a fractal, and if we coarse grain the phase space, it will appear that Γ is growing. As a definition of coarse graining, if one takes every point in the phase space and surrounds it by solid spheres of fixed volume, the union of those spheres is the “coarse grained” volume of phase space, which indeed grows. This is the origin of the second law of thermodynamics. This is illustrated in Figure 1.1.
In quantum mechanics, the conservation of information is expressed as
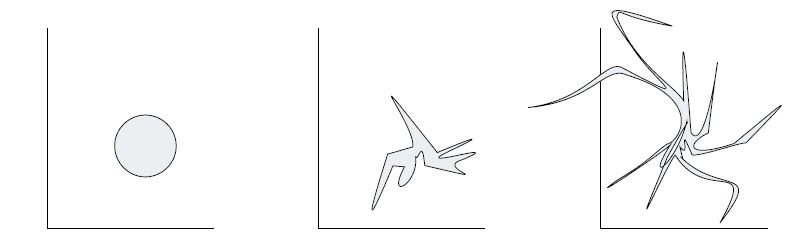
Fig. 1.1. Evolution of a fixed volume in phase space.
the unitarity of the S-matrix .If we again approach a system with limited knowledge, we might express this by a projection operator onto a subspace, P, instead of a definite state. The analog of the phase space volume is the dimensionality of the subspace
N = Tr P
The unitarity of the time evolution insures that N is conserved with time.
A more refined definition of information is provided by the concept of entropy. Suppose that instead of specifying a region Γ in phase space, we instead specify a probability density ρ(p, q) in phase space. A generalization of the volume is given by the exponential of the entropy VΓ → exp S, where
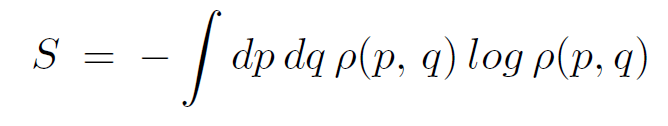 (1.1)
(1.1)
It is easy to check that if ρ = 1/VΓ inside Γ and zero outside, then S = log VΓ. Similarly, for quantum mechanics the sharp projector P can be replaced by a density matrix ρ. In this case the fine grained or Von Neumann entropy is
 (1.2)
(1.2)
For the case ρ = P/Tr P the entropy is log N. Thus the entropy is an estimate of the logarithm of the number of quantum states that make up the initial ensemble. In both quantum mechanics and classical mechanics the equations of motion insure the exact conservation of S for a closed, isolated system.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|