We have already seen in the thought experiment discussed in the previous section that ħ enters the scene. That Planck's constant has to play a role can also be seen from the First Law:

.

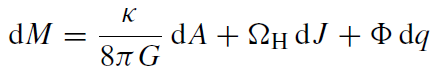Since T_BH dS_BH = κ/(8πG) dA, one must have

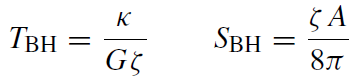
with an undetermined factor ζ . What is the dimension of ζ? Since SBH has the dimension of Boltzmann's constant k_B, k_B/ζ must have the dimension of a length squared. There is, however, only one fundamental length available, the Planck length

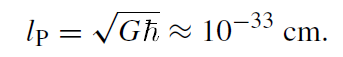 (1.1)

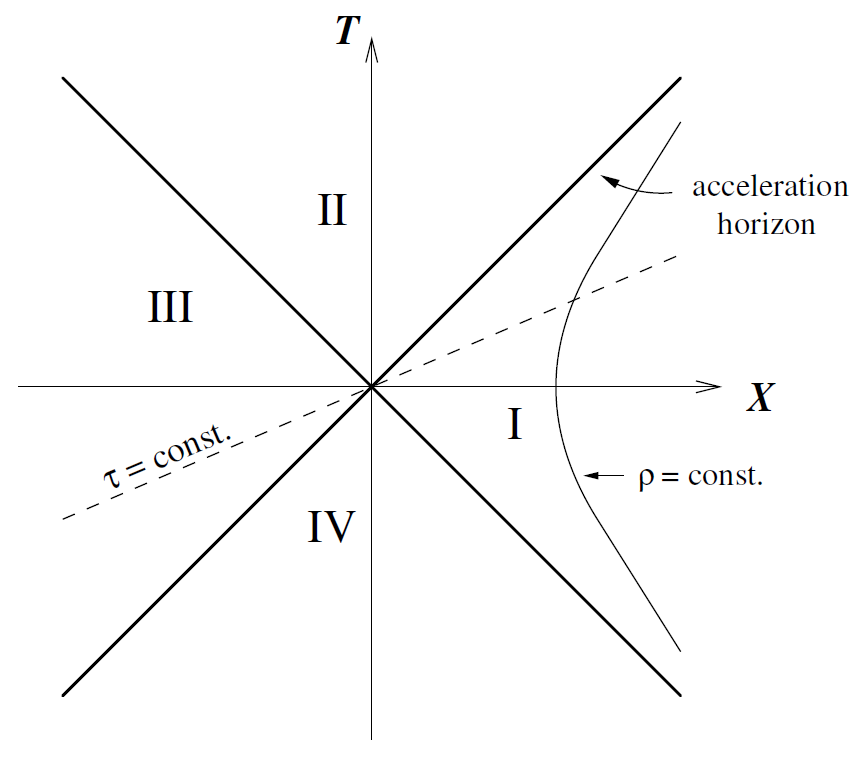
Figure 1.1. Uniformly accelerated observer in Minkowski space.

(For string theory, this may be replaced by the fundamental string length.) Therefore,

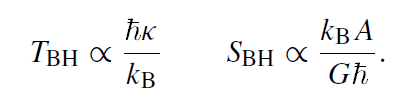 (1.2)

The precise factors in (1.2) were determined in a pioneering paper by Hawking (1975). The key ingredient in his discussion is the behaviour of quantum fields on the background of an object collapsing to form a black hole. Similar to the situation of an external electric field (Schwinger effect), there is no uniquely defined notion of a vacuum. This leads to the occurrence of particle creation. The peculiarity of the black hole case is the thermal distribution of the particles created.

There exists an analogous effect already in flat spacetime, discussed by Unruh (1976), with earlier related work by Fulling (1973) and Davies (1975). In the following I shall briefly describe this effect.

Whereas all inertial observers in Minkowski space agree on the notion of vacuum (and therefore on particles), this no longer holds for non-inertial observers. Consider an observer who is uniformly accelerating along the X-direction in (1 + 1)-dimensional Minkowski spacetime (figure 1.1). The Minkowski Cartesian coordinates are labelled here by upper-case letters. The orbit of this observer is the hyperbola shown in figure 1.1. One recognizes that, as in the Kruskal diagram for the Schwarzschild metric, the observer encounters a horizon (here an ‘acceleration horizon’). There is, however, no singularity behind this horizon. Region I is a globally hyperbolic spacetime on its own the so called Rindler spacetime. This spacetime can be described by coordinates (τ, ρ) which are connected to the Cartesian coordinates via the coordinate transformation

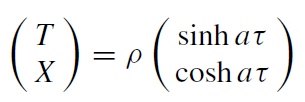 (1.3)

where a is a constant (the orbit in figure 1.1 describes an observer with acceleration a, who has ρ = 1/a). Since

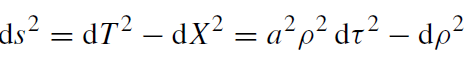 (1.4)

the orbits ρ = constant are also orbits of a timelike Killing field ∂/∂τ. It is clear that τ corresponds to the external Schwarzschild coordinate t and that ρ corresponds to r . As in the Kruskal case, ∂/∂τ becomes spacelike in regions II and IV.

The analogy with Kruskal becomes even more transparent if the Schwarzschild metric is expanded around the horizon at r = 2GM. Introducing ρ²/(8GM) = r − 2GM  one has

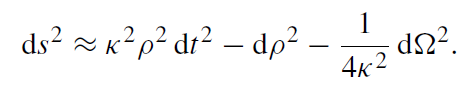 (1.5)

Comparison with (1.4) shows that the first two terms on the right-hand side of (1.5) correspond exactly to the Rindler spacetime (1.4) with the acceleration a replaced by the surface gravity κ. The last term in (1.5) describes a two-sphere with radius (2κ)⁻¹.

How does the accelerating observer experience the standard Minkowski vacuum 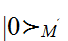? The key point is that the vacuum is a global state correlating regions I and III in figure 1.1 (similar to Einstein-Podolsky-Rosen correlations), but that the accelerated observer is restricted to region I. Considering, for simplicity, the case of a massless scalar field, the global vacuum state comprising the regions I and II can be written in the form

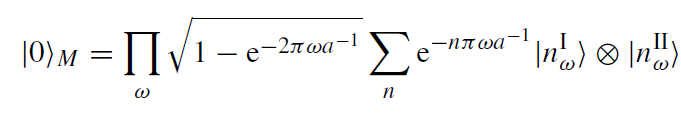 (1.6)

where 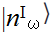and 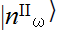are n-particle states with frequency ω = |k| in regions I and II, respectively. Expression (1.6) is an example of the Schmidt expansion of two entangled quantum systems, see, e.g., Giulini et al (1996); note also the analogy of (1.6) with a BCS state in the theory of superconductivity.

For an observer restricted to region I, state (1.6) cannot be distinguished, by operators with support in I only, from a density matrix that is found from (1.6) by tracing out all degrees of freedom in region II,

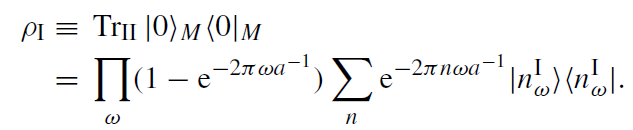 (1.7)

Note that the density matrix ρ_I has exactly the form corresponding to a thermal canonical ensemble with temperature

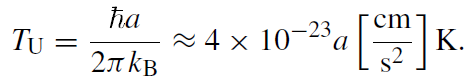 (1.8)

An observer who is accelerating uniformly through Minkowski space thus sees a thermal distribution of particles. This is an important manifestation of the non-uniqueness of the vacuum state in quantum field theory, even for flat spacetime. A more detailed discussion invoking models of particle detectors confirms this result.

The ‘Unruh temperature’ (1.8), although being very small for most accelerations, might be observable for electrons in storage rings where spin precession is used as a ‘detector’ (Leinaas 2001). Due to the circular nature of the accelerator, the spectrum of the observed particles is not then thermal. Since this would complicate the direct comparison with the Hawking effect, other proposals for measuring (1.8), for example by means of ultra-intense lasers (Chen and Tajima 1999), also exist.

I shall now turn to the case of black holes. From the form of the line element near the horizon, (1.5), one can already anticipate that according to the equivalence principle a black hole radiates with a temperature as specified in (1.8) with a being replaced by κ. This is, in fact, what Hawking (1975) found. The temperature reads:

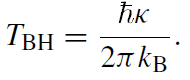 (1.9)

For the total luminosity of the black hole one finds

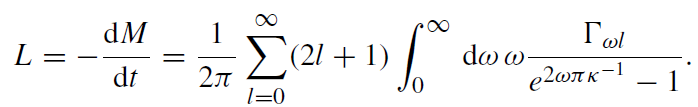 (1.10)

The term Γ_ωl called the ‘grey body factor’ because it encodes a deviation from the black body spectrum takes into account the fact that some of the particle modes are backscattered into the black hole by means of spacetime curvature. For the special case of the Schwarzschild metric where κ = (4GM)⁻¹, (1.9) becomes

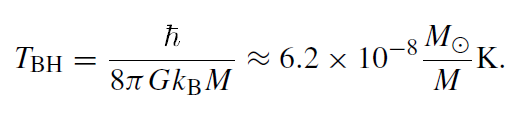 (1.11)

For solar mass black holes (and even more so for the Galactic black hole), this is of course utterly negligible the black hole absorbs much more from the ubiquitous 3K-microwave background radiation than it radiates itself.

One can, however, estimate the lifetime of a black hole by making the plausible assumption that the decrease in mass is equal to the energy radiated to infinity. Using the Stefan–Boltzmann law, one gets

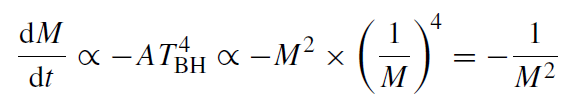
which, when integrated, yields

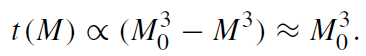 (1.12)

Here M₀ is the initial mass. It has been assumed that after the evaporation M << M₀. Very roughly, the lifetime of a black hole is thus given by

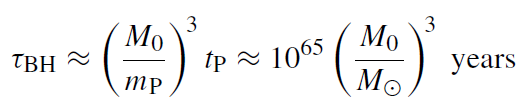 (1.13)

(m_P and t_P denote Planck mass and Planck time: m_P = ħ/l_P, t_P = l_P). The Galactic black hole thus has a lifetime of about 3 × 10⁸⁵ years! If in the early universe primordial black holes with M₀ ≈ 5 × 10¹⁴ g were created, they would evaporate at the present age of the universe.

A very detailed investigation into black hole evaporation was made by Page (1976). He found that for M >> 10¹⁷ g the power emitted from an (uncharged, non-rotating) black hole is

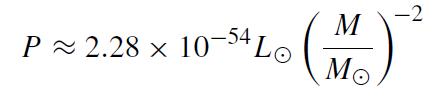
81.4% of which is in neutrinos (he considered only electron- and muon neutrinos), 16.7% in photons, and 1.9% in gravitons, assuming that there are no other massless particles around. Since a black hole emits all existing particles in Nature, this result would be changed by the existence of massless supersymmetric or other particles. In the range 5 × 10¹⁴ g << M << 10¹⁷ g, Page found

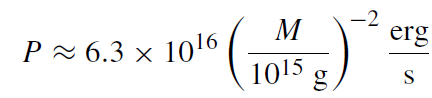
45% of which is in electrons and positrons, 45% in neutrinos, 9% in photons, and 1% in gravitons. Massive particles with mass m are only suppressed if  k_BT_BH < m. For   M < 5 × 10¹⁴ g higher-mass particles are also emitted.

All of these derivations use the approximation that the spacetime background remains classical. In a theory of quantum gravity, however, such a picture cannot be maintained. Since the black hole becomes hotter while radiating, see (1.11), its mass will eventually enter the quantum-gravity domain M ≈ m_P, where the semiclassical approximation breaks down. The evaporation then enters the realm of speculation. As an intermediate step one might consider the heuristic ‘semiclassical’ Einstein equations,

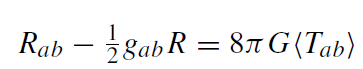 (1.14)

where on the right-hand side the quantum expectation value of the energy-momentum tensor appears. The evaluation of 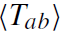 which requires regularization and renormalization is a difficult subject on its own (Frolov and Novikov 1998). The renormalized  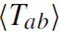is essentially unique (its ambiguities can be absorbed in coupling constants) if certain sensible requirements are imposed. Evaluating the components of the renormalized  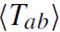near the horizon, one finds that there is a flux of negative energy into the hole. Clearly this leads to a decrease of the black hole's mass. These negative energies represent a typical quantum effect and are well known from the accurately measured Casimir effect. This occurrence of negative energies is also responsible for the breakdown of the classical area law.

The negative flux near the horizon also lies at the heart of the ‘pictorial’ representation of Hawking radiation that is often used, see, e.g., Parikh and Wilczek (2000). In vacuum, virtual pairs of particles are created and destroyed. However, close to the horizon, one partner of this virtual pair might fall into the black hole, thereby liberating the other partner to become a real particle and escaping to infinity as Hawking radiation. The global quantum field exhibits quantum entanglement between the inside and outside of the black hole, similar to the case of the accelerated observer discussed earlier.

I want to end this section by giving explicit expressions for the Hawking temperature (1.6) in the case of rotating and charged black holes. For the Kerr solution, one has

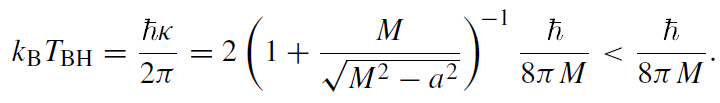 (1.15)

Rotation thus reduces the Hawking temperature. For the Reissner-Nordstrom solution (describing a charged spherically symmetric black hole) one has

 (1.16)

Thus, electric charge also reduces the Hawking temperature. For an extremal black hole, r₊ = GM =√G |q|, and thus T_BH = 0.