المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | مجموع ريمان Rieman Sum |
 2082
 02:02 صباحاً
التاريخ: 7-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 287-288|
أقرأ أيضاً
التاريخ: 2-11-2015
1223
التاريخ: 27-10-2015
17745
التاريخ: 2-11-2015
3285
التاريخ: 3-11-2015
1359
|
يجسد هذا المجموع فكرة إيجاد مساحات الأشكال الهندسية الواقعة في المستوى الديكارتي والذي يكون محور السينات أحد اطرافها كما في الشكل .
وفي بعض الأحيان يكون محور الصادات كأحد أضلاعها . بطريقة تجزئتها إلى مستطيلات قواعدها أطوال .
الفترات الجزئية س]س ر-1,س ر[ والتي تساوي كل منها س ر-س ر1- وحدة طول وارتفاعها قيم الاقتران ق(س+ر)
وينسب هذا المجموع إلى الرياضي الألماني ريمان (1826 – 1866)م ويعبر عنه بالصورة .
حيث ق : اقتران حقيقي متصل على الفترة [ أ ، ب ] .
6ن : فجزئه منتظمة للفترة [ أ ، ب ] ومن مجموع ريمان انبثق التكامل المحدود وعلى الصورة .
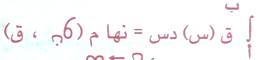حيث ʃ هي الحرف الأول من كلمة Sum المذكورة أعلاه .
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
