المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | اختبار الخط الرأسي Vertical line Experiment |
 18239
 04:19 مساءاً
التاريخ: 27-10-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 13-14|
أقرأ أيضاً
التاريخ: 6-11-2015
1278
التاريخ: 7-12-2015
2640
التاريخ: 19-11-2015
1531
التاريخ: 3-12-2015
1836
|
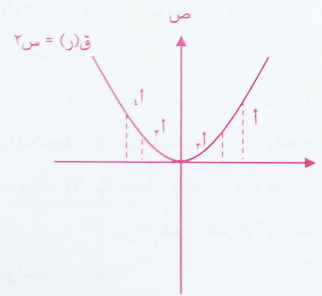
هذا الاختبار يميز بين العلاقة والاقتران , فعند تمثيل المنحني بيانياً , فإذا كان أي خط رأسي مرسوم على المنحني لا يقطعه إلا في نقطة واحدة فقط فإن هذا المنحنى الاقتران كما في الشكل .
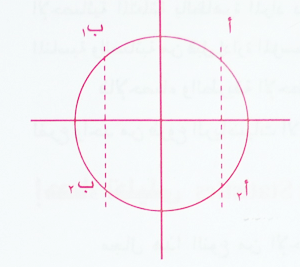
أما منحني المعادلة س2+ص4=ر2 والتي تمثل الدائرة التي مركزها م (0 , 0) ونصف قطرها ر وحدة . نلاحظ ان كل خط رأسي يقطع المنحني في نقطتين (أكثر من نقطة) فالمنحني هو لعلاقة
ومنه س2+ص4=ر2 علاقة .
|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
طلبة الجامعات العراقية يرددون عهد الولاء للوطن عند مرقد أبي الفضل العباس (عليه السلام)
|
|
|
