المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | قانون جيب التمام Cosine Rule |
 6352
 09:09 صباحاً
التاريخ: 23-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 231|
أقرأ أيضاً
التاريخ: 9-2-2017
1269
التاريخ: 21-12-2015
4613
التاريخ: 10-11-2015
1209
التاريخ: 13-11-2015
14339
|
انه قانون يربط اضلاع المثلث بزواياه كما يلي :
للمثلث أ ب جـ
حيث زواياه : 
أ,ب,ج
واضلاعه أ َ ، ب َ ، جـ َ كما في الشكل
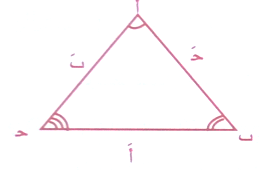
فإن :
(أَ) = (بَ)2 + (جـَ)2 – 2 بَ جـ َ جتا أ .
وكذلك (بَ)2 = (أَ)2 + (جـَ)2 – 2 أَ جـَ جتا ب
وكذلك (جـَ)2 = ( أَ)2 + (بَ)2 – 2 أَ بَ جتا جـ
ويستخدم هذا القانون في حل المثلث أي إيجاد قياسات زوايا وأطوال اضلاعه الغير معلومة .
|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|
