Delimitation and predication

On the basis of the previous considerations we are led to a distinction of two rather different types of semantic elements applying to the reference variables X_i. The first type delimits the set substitutable for the variable X_i, the second type represents the properties and relations predicated of the elements of this set. Before turning to problems of the latter elements, I will make some remarks concerning the former. These are essentially the elements which constitute the readings of articles, quantifiers, and similar syntactic formatives. And though many attempts to arrive at a syntactic account of the interrelated phenomena of reference and delimitation have been made (with no conclusive result so far), very little is known with respect to the question how the semantic problems involved are to be dealt with.

Notice first of all that delimiting features have a status completely different from that of predicating features. While these specify the conditions to be met by the objects of the set referred to, delimiting features do not apply to these objects as such, but to the set as a whole, specifying its size - relative or absolute - its role in the discourse, etc. In order to make this distinction somewhat more precise we may compare the delimiting features with certain operators introduced in modern logic. We will do this by means of some examples.

Consider first the feature ‘ Definite ’. This feature, characteristically realized by the definite article in languages displaying articles, indicates that the set forming the reference instance is already given and uniquely identifiable by means of the respective predicative features. ‘ Definite ’ thus corresponds in a sense to the iota-operator which forms definite descriptions. But whereas the iota-operator is bound to unique individuals, the feature Definite applies to uniquely specified sets - those containing one element being a special case. Thus Definite comprises in a sense also the lambda-operator which forms the class of precisely those elements exhibiting the property represented by a given predicate. But whereas the iota- and the lambda- operator yield expressions of different types - viz. individuals and classes respectively -, an expression formed by means of the feature Definite is always of the same type, irrespective of the number of elements in the set Xi to which Definite applies. This is a direct consequence of the digression from the quantification theory. It allows for a natural treatment of the complete parallelism in sentences like ‘ The boy came ’ and ‘ The boys came ’.

The correspondence between the feature Definite and the iota-operator has its counterpart in the correspondence between the feature Definite ’ or ‘ Indefinite ’ and the eta-operator, which forms indefinite descriptions. (For indefinite descriptions see e.g. Reichenbach, 1966, p. 265.) The term ‘Indefinite’ is extremely misleading, however, as in a sentence like ‘A boy came ’ no vagueness or indefiniteness is involved. Rather a particular set of (one or more) elements is introduced and might be taken up later on by means of the feature Definite. I will therefore use the term ‘ Specifying ’ which should be understood as selecting a particular fraction of the universe which has not been referred to previously.¹ The feature Indefinite on the other hand might be more appropriate for the treatment of the following by now well known phenomenon:

(21) is ambiguous with respect to the status of the NP₁ ‘ a newspaper ’: if continued by (22 a) the set X₁ is introduced by the feature Specifying which constitutes a fixed object also for future reference, taken up by the NP₁ ‘it’ in (22a). In this case James was asking for a particular newspaper, say the Prawda from 1 May 1967. If (21) is continued by (22b), then NP1 remains unspecified, it does not constitute a fixed object. Therefore the corresponding NP in (22b) cannot refer to the same set. In this case X₁ in the reading of (21) is bound by the feature Indefinite. Notice that the indefinite article represents the feature Indefinite in the sense illustrated here only if it appears within the scope of intentional verbs like ‘ask for’, ‘ want’, ‘look for’, ‘will’, etc., or of the negation.²

After this extremely provisional illustration of delimiting features like Definite, Specifying, Indefinite, etc. we may ask how they are to be incorporated into semantic representations. I have no definite answer to this question, but I will briefly present two alternatives indicating the lines along which, in my opinion, a solution might be constructed. Let Q be a variable over the features in question. Every feature of this type applies to precisely one argument X_i. We will write now (QX_j) for the application of Q to X_i thereby forming an operator which specifies X_i in the way represented by Q. This operator may now be introduced into semantic representations in one of two ways: (i) we prefix it to the reading of the whole sentence (or at least the next higher constituent) of which the corresponding NP_i is a constituent. In this case the status of (QX_i) is analogous to that of the existential (and universal) quantifier of logical systems; (ii) we prefix it to the reading of the NP_i itself. In this case the status of (QX_i) is parallel to that of the iota- and eta-operator of logical systems. It forms terms which function as arguments for other predicative features. The operations combining readings of syntactically related constituents and the form of the resulting readings are different in both cases. In the case of (i) only the argument X_i of an NP_i is to be substituted for the variables of the related constituents, while the operator (QX_i) is prefixed to the whole resulting reading. In the case of (ii) the whole reading of the NP_i, beginning with the operator (QX_i) is to be substituted for the pertinent variables. Thus the reading of (13 a) ‘The boys saw the girls’ as abbreviated in (14 a) would be (23) according to (i) and (24) according to (ii). We use brackets to indicate the scope of the (QX_i):

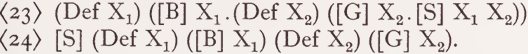
The alternative (ii) and the corresponding representation (24) is similar to Katz’ recent proposal according to which the readings of the whole subject-NP and object-NP are substituted for corresponding variables within the reading of the verb. The operator (QX_i) that we have introduced, however, gives a clear representation of the fact that the argument of a given NP but not its complete reading is an argument of the semantic features of the verb. The latter interpretation would lead to a completely wrong higher level predication.³

The choice between (i) and (ii), if these are reasonable alternatives at all, depends on unsolved problems of both syntactic and semantic structure. The former are mainly those of the internal structure of NPs, in particular of the deep structure status of restrictive relative clauses. There are serious doubts whether relative clauses can be an internal subconstituent of the NP which they restrict, since this solution, which has been accepted until recently, leads to certain absurdities. The most crucial difficulty which has been noticed by several authors originates with relative clauses that contain each other. An example is

(25) [A boy [who bought [a book [that pleased [him]NP₁]S’]NP₂]S”]NP₁ finally got rid of [it]NP₂

where the NPs underlying the pronouns ‘him’ and ‘it’ would contain an infinite alternating selfembedding of S' and S", if relative clauses are part of them. The solution of this and similar problems is obviously relevant to the treatment of the (QX_i). The alternative (ii) seems to be unnatural or even inapplicable if restrictive relative clauses must in general be removed from the NPs they modify.

The semantic problems on which the choice between (i) and (ii) depends comprise among other things the behavior of (QX_i) with respect to negation. Consider the following paradigm:

(26) (a) It is not true that the girl trusted him.

(b) The girl didn’t trust him.

(27) (a) It is not true that a girl trusted him.

(b) A girl didn’t trust him.

(c) No girl trusted him.

(26 a) and (26 b) are synonymous in the sense that identical truth conditions are associated with them. The situation is more complicated with the sentences under (27). In its normal interpretation (27 a) is synonymous with (27 c), but not with (27 b). A plausible account for this difference seems to be the assignment of In¬ definite to ‘a girl’ in (27 a) and Specifying to ‘a girl’ in (27 b). Thus (27 b) is the negation of ‘A girl trusted him’ with a specifying article ‘a’, whereas (27 c) (and (27 a)) is the negation of the nonexisting homophonous sentence with indefinite ‘a’.⁴ This means that, given a negated sentence, (Indef X_i) is always within the scope of negation, whereas (Spec X_i) never is. In other words, there is a certain trading relation between (Indef X_j) and (Spec X_i) with respect to negation. No such trading exists with respect to (Def X_i). Hence the lack of (26 c). Any revealing account of this different behavior of the features discussed clearly bears on the choice between (i) and (ii) above. We may face even the possibility that both alternatives are required, some operators being treated according to (i), others according to (ii).

A further set of rather complicated problems arises from the fact that quantifications also have the function of delimiting the X_i. They do this, however, in a way different from that of the specifying features discussed so far. Quantifications comprise first of all the cardinal numbers, but also indefinite quantifications like ‘many’, ‘few’, ‘some’. Let us briefly consider first the status of numbers. Since we have claimed above that the X_i represent sets, not individuals, and that the delimiting features apply to these sets as a whole, not to the elements contained in it, we get a natural representation of the fact that numbers are properties of sets, irrespective of other properties of their elements, and not properties of individuals. But whereas numbers are usually treated in the predicate calculus as second level predicates, which are predicated only of the predicates ascribed to the primary arguments, we will apply them to the arguments directly, as these are sets, not individuals. This consideration brings out the difference between predicative and delimitative features more clearly: specifying the properties of the elements and the scope of reference respectively, they represent, so to speak, two aspects of abstraction simultaneously.

Numbers may be combined now with the features Definite, Specifying, and Indefinite, as illustrated in the following examples:

(28) (a) He was looking for the two dollars and he found them.

(b) He was looking for two dollars and he found them.

(c) He was looking for two dollars and he found two.

There is, moreover, overwhelming evidence that in general the so-called indefinite article in English and several other languages is nothing but the unstressed realization of the numeral ‘one’. For details see Perlmutter (1970). In other words, the features Specifying and Indefinite are not assigned to a separate phonemic matrix, whereas Definite is overtly realized in most cases. The formal representation of the combination of numbers with the features discussed above is a difficult problem, depending again in part on the behavior with respect to negation. I cannot go into these details here. We simply assume for the present discussion that the Q in the operators (QX_i) is a variable not only over Def, Indef, and Spec, but also over combinations of these with numerals, the precise nature of this combination being left open.

Indefinite quantifications like ‘many’, ‘few’, ‘some’ are similar to numerals in many respects, the main difference being that they provide no absolute quantification, but one which is relative to a certain norm.

Notice that features representing absolute or relative quantification can to a certain extent be combined with true predicative features in a way characteristic for such predicative elements. Thus we have ‘very many books’ alongside with ‘very good books’. Other cases are ‘more than fifty books’, ‘at most fifty books’, etc. This complicates the internal semantic structure of the (QX_i) still further.

A particular combination of quantifying features and those specifying reference instances appear in the readings of ‘all’, ‘every’, ‘each’, ‘any’, and the determiner constituents of the different types of generic NPs. What they have in common seems to be the fact that they may or must relate the set X_ix to the complete class characterized by the pertinent predicative features, a relation which is not involved in absolute and relative quantification. This is accomplished however in completely different ways resulting in similarly different consequences. Consider e.g. the following sentences:

(29) (a) [Every logician]NP1 would infer that.

(b) [All logicians]NP1 would infer that.

(c) [Logicians]NP1 would infer that.

(d) [A logician]NP1 would infer that.

(e) [The logician]XP1 would infer that.

One might perhaps argue that these sentences are synonymous in one reading in the sense that identical truth conditions are associated with this reading. I have some doubts in this respect, however. In any case, the truth conditions are arrived at by means of completely different operations. The X₁ of (29 a), e.g., is a set consisting of one element, and the delimiting features of ‘ every’ represent an instruction which might be paraphrased as ‘substitute for this element the representation of each single object such that the conditions expressed by “logician” are met’. The X₁ of (29 b) on the other hand consists of a representation of the class of logicians and the delimiting features of ‘ all ’ represent an instruction to the effect that predicates assigned to X₁ apply to all elements of this class. That these loosely indicated operations may have different results is brought out quite clearly by the following examples:

(30) (a) [Every student of our college]Np1 likes baseball.

       (b) [All students of our college]NP1 like baseball.

(31) (a) [Every student of our college]NP1 performs a play.

      (b) [All students of our college]NP1 perform a play.

Whereas (30 a) and (30 b) are synonymous, (31 a) and (31 b) are not, (31 a) requiring as many one-man-performances as there are students. I will not pursue the problems of universal and generic sentences any further, as they constitute a large topic on their own. Let me add only that the operators involved behave differently again with respect to negation: the sentences (29 b) and (29 c) are at least similar in meaning in a way in which (32 a) and (32 b) are not, these being synonymous with (33 a) and (33 b) respectively:

(32) (a) It is not true that all logicians would infer that.

(b) It is not true that logicians would infer that.

(33) (a) Not all logicians would infer that.

(b) Logicians would not infer that.

Let me summarize briefly the lengthy and inconclusive discussion of delimitations. We first assumed that the reference indices i correspond to variables X_i functioning as arguments of the predicative features. These variables range over sets of possible objects which must meet the conditions represented by the predicative features. We then faced the necessity of elements delimiting the sets to be substituted for the X_i. These delimiting elements have a status completely different from that of the predicative elements. The delimiting features form operators of the form (QX_i) where the Q is a variable over (complexes of) those features. For each NP_i of the deep structure there is precisely one (QX_i) prefixed to the reading either of that NP_i or of a constituent containing that NP_i.⁵ The delimiting features in turn subdivide into quantifying and specifying elements. The former represent absolute, relative, and universal characteristics of the extension or scope of the set to be substituted for the X_i. The latter represent instructions to pick up the set referred to in one or the other way. Specifying and quantifying features are combined in a still unexplored way to form the operators (QX_i). The quantifying features may also be modified by certain predicative features, this modification being governed by the principles pertinent to the combination of predicative features in general.

It is worth noting that our interpretation of the arguments X_i and the pertinent delimitations, which is based so far on observations concerning countable objects, accounts at the same time in a very plausible way for mass objects:

(34) (a) [The juice you gave me]NP1 was excellent.

(b) [Water] NP1 is still missing.

(c) Would you like [some coffee]NP1?

(d) [All iron]NP1 rusts.

The X1 of these examples is to be substituted simply by the representation of improper sets, as it were, which cannot be individualized at all, since they are not conceived as consisting of individuals. From this it follows immediately that certain quantifications do not apply. (This restriction must be derived from the inherent semantic and/or syntactic features of the respective nouns in a way not to be discussed here.) All other decisions however remain unchanged: the predicative features apply to the elements of the set X1 referred to, i.e. to a single improper object in this case. Quantifying features concern the set as a whole. And the selection of the appropriate referent represented by the specifying features is as usual. Thus the features Def, Spec, and Indef account for (34 a), (34 b) and (34 c), respectively. And the operation represented by ‘ all ’ works for (34 d) in the same way as for (29 b), (30 b), and (31 b).

¹ The proposed element ‘ Specifying ’ corresponds closely to the referential operator introduced in Bellert (1969), the main difference being the fact that Bellert’s operator applies to individuals, whereas Specifying introduces sets of individuals. - It goes without saying that Definite and Specifying are not negations of each other, as the notation ‘ ± Definite ’ would suggest by its parallelism to such features as ‘ ± Human ’ etc. In fact, the element Definite is not subject to negation at all.

² The phenomena connected with have been discussed recently by several writers. The latest treatment known to me is that of Karttunen (1968). The distinction between the two readings of (21) is explained there by assuming an individual constant for the continuation (22 a) and an individual variable bound by an existential quantifier for the continuation (22 b) There are several objections, however, even if we ignore the fact that sets instead of individuals are required for reference. Firstly, sentence types, which are the only object of linguistic analysis, cannot contain individual constants, but only variables to be replaced by constants if the sentence is used in a particular discourse. Secondly, a constant would be required also in the case of definiteness. Thus the distinction between the definite and indefinite article would be obscured. And thirdly, the claim of existence expressed by the existential quantifier is not justified. In a sentence like ‘John was looking for a tack, but he didn’t find one’ nothing is presupposed or asserted with respect to the existence of a tack in that spatial area where his looking for was to take place. The only claim is that John presumed the possible existence of a tack. Notice that this has nothing to do with ontological problems. The same consideration applies with respect to fictitious objects: ‘ The witch was looking for a unicorn, but she couldn’t see one.’

³ Notice that the alternatives (i) and (ii) correspond somehow to the definiens and the definiendum of the definition by which the iota-operator is usually introduced: the formula

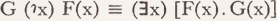
where F is a unique function and G(x) an arbitrary propositional function would be parallel to the equivalence

where Q and Q' are the delimiting features according to interpretation (ii) and (i) respectively.

⁴ It is worth noting that (27 b) and (27 c) are in a sense analogous to the two possible scopes of negation in indefinite descriptions (see e.g. Reichenbach 1966, pp. 262 ff): given the formula (a) then its negation (b) can be interpreted either as (c) or (d), if no convention for the scope of negation is stated, (c) and (d) are not equivalent, however, as can be seen from their reformulation as (e) and (f) respectively:

With respect to (Indef X_i), the scope interpretation would then be analogous to (d) and its equivalent (f), as can be seen from (27 a) and (27 c). The problem of ambiguous scope arises with respect to the iota-operator, if F is not a unique function, i.e. in the case of improper definite descriptions. Since this possibility is excluded by definition with respect to Definite and Specifying, whose argument X_i is always uniquely given, there is only one possible effect of negation. This is expressed by sentences of the type (26 b) and (27 b) respectively.

⁵ An exception to this statement are predicative NPs in sentences like ‘John is a doctor’ which do not identify but describe the referent of the subject NP. Such predicate nouns do not provide a new reference instance. They differ from all other NPs in other respects as well and must be treated separately in any case.