


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 1-2-2016
التاريخ: 19-2-2016
التاريخ: 15-12-2016
التاريخ: 9-3-2021
|
First, we notice that if we have a rotation in three dimensions, whether of a rigid body or any other system, what we deduced for two dimensions is still right. That is, it is still true that xFy−yFx is the torque “in the xy-plane,” or the torque “around the z-axis.” It also turns out that this torque is still equal to the rate of change of xpy−ypx, for if we go back over the derivation of Eq. (18.15) from Newton’s laws we see that we did not have to assume that the motion was in a plane; when we differentiate xpy−ypx, we get xFy−yFx, so this theorem is still right. The quantity xpy−ypx, then, we call the angular momentum belonging to the xy-plane, or the angular momentum about the z-axis. This being true, we can use any other pair of axes and get another equation. For instance, we can use the yz-plane, and it is clear from symmetry that if we just substitute y for x and z for y, we would find yFz−zFy for the torque and ypz−zpy would be the angular momentum associated with the yz-plane. Of course, we could have another plane, the zx-plane, and for this we would find zFx−xFz=d/dt(zpx−xpz).
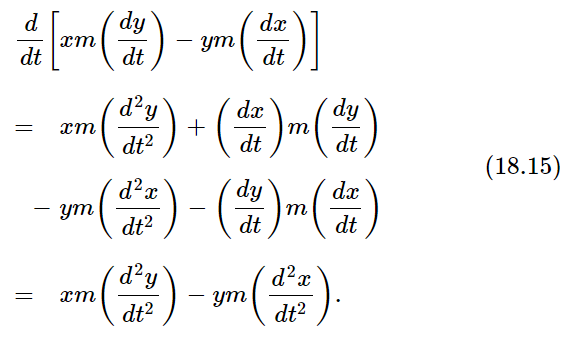
That these three equations can be deduced for the motion of a single particle is quite clear. Furthermore, if we added such things as xpy−ypx together for many particles and called it the total angular momentum, we would have three kinds for the three planes xy, yz, and zx, and if we did the same with the forces, we would talk about the torque in the planes xy, yz, and zx also. Thus we would have laws that the external torque associated with any plane is equal to the rate of change of the angular momentum associated with that plane. This is just a generalization of what we wrote in two dimensions.
But now one may say, “Ah, but there are more planes; after all, can we not take some other plane at some angle, and calculate the torque on that plane from the forces? Since we would have to write another set of equations for every such plane, we would have a lot of equations!” Interestingly enough, it turns out that if we were to work out the combination x′Fy′−y′Fx′ for another plane, measuring the x′, Fy′, etc., in that plane, the result can be written as some combination of the three expressions for the xy-, yz- and zx-planes. There is nothing new. In other words, if we know what the three torques in the xy-, yz-, and zx-planes are, then the torque in any other plane, and correspondingly the angular momentum also, can be written as some combination of these: six percent of one and ninety-two percent of another, and so on. This property we shall now analyze.
Suppose that in the xyz-axes, Joe has worked out all his torques and his angular momenta in his planes. But Moe has axes x′,y′,z′ in some other direction. To make it a little easier, we shall suppose that only the x- and y-axes have been turned. Moe’s x′ and y′ are new, but his z′ happens to be the same. That is, he has new planes, let us say, for yz and zx. He therefore has new torques and angular momenta which he would work out. For example, his torque in the x′y′-plane would be equal to x′Fy′−y′Fx′ and so forth. What we must now do is to find the relationship between the new torques and the old torques, so we will be able to make a connection from one set of axes to the other. Someone may say, “That looks just like what we did with vectors.” And indeed, that is exactly what we are intending to do. Then he may say, “Well, isn’t torque just a vector?” It does turn out to be a vector, but we do not know that right away without making an analysis. So in the following steps we shall make the analysis. We shall not discuss every step in detail, since we only want to illustrate how it works. The torques calculated by Joe are
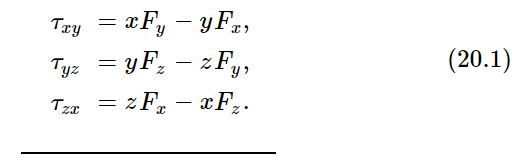
We digress at this point to note that in such cases as this one may get the wrong sign for some quantity if the coordinates are not handled in the right way. Why not write τyz=zFy−yFz? The problem arises from the fact that a coordinate system may be either “right-handed” or “left-handed.” Having chosen (arbitrarily) a sign for, say τxy, then the correct expressions for the other two quantities may always be found by interchanging the letters xyz in either order
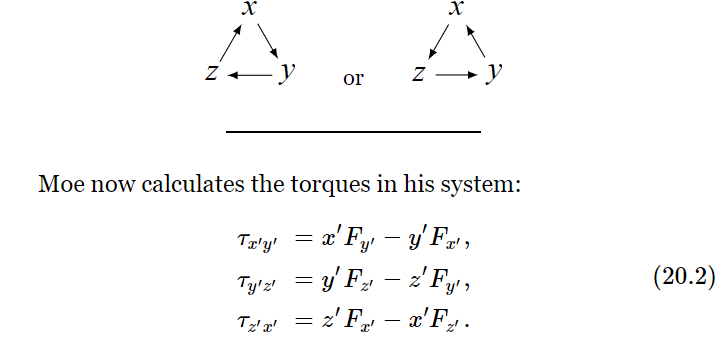
Now we suppose that one coordinate system is rotated by a fixed angle θ, such that the z- and z′-axes are the same. (This angle θ has nothing to do with rotating objects or what is going on inside the coordinate system. It is merely the relationship between the axes used by one man and the axes used by the other, and is supposedly constant.) Thus, the coordinates of the two systems are related by
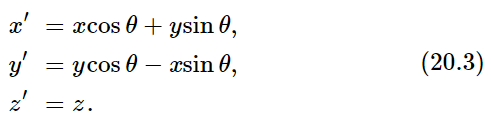
Likewise, because force is a vector it transforms into the new system in the same way as do x, y, and z, since a thing is a vector if and only if the various components transform in the same way as x, y, and z:
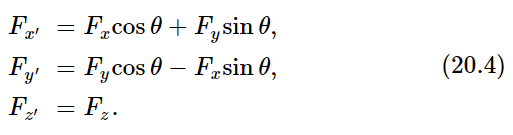
Now we can find out how the torque transforms by merely substituting for x′, y′, and z′ the expressions (20.3), and for Fx′, Fy′, Fz′ those given by (20.4), all into (20.2). So, we have a rather long string of terms for τx′y′ and (rather surprisingly at first) it turns out that it comes right down to xFy−yFx, which we recognize to be the torque in the xy-plane:
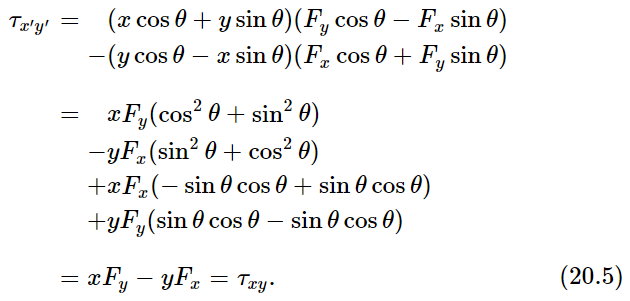
That result is clear, for if we only turn our axes in the plane, the twist around z in that plane is no different than it was before, because it is the same plane! What will be more interesting is the expression for τy′z′, because that is a new plane. We now do exactly the same thing with the y′z′-plane, and it comes out as follows:
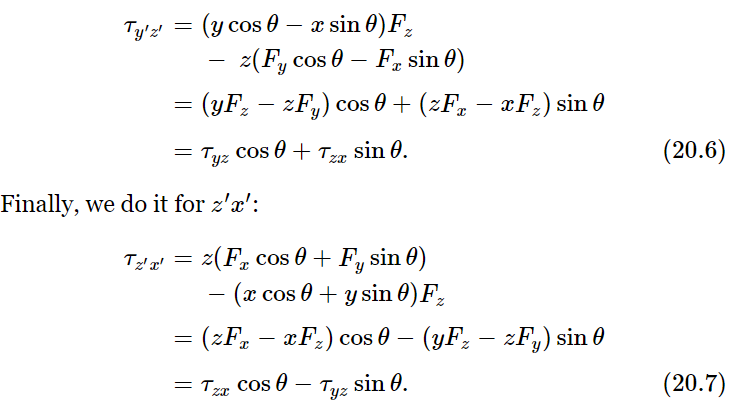
We wanted to get a rule for finding torques in new axes in terms of torques in old axes, and now we have the rule. How can we ever remember that rule? If we look carefully at (20.5), (20.6), and (20.7), we see that there is a close relationship between these equations and the equations for x, y, and z. If, somehow, we could call τxy the z-component of something, let us call it the z-component of τ, then it would be all right; we would understand (20.5) as a vector transformation, since the z-component would be unchanged, as it should be. Likewise, if we associate with the yz-plane the x-component of our newly invented vector, and with the zx-plane, the y-component, then these transformation expressions would read
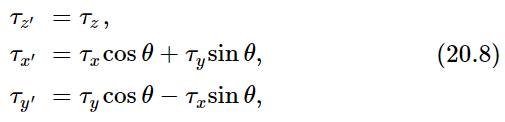
which is just the rule for vectors!
Therefore, we have proved that we may identify the combination of xFy−yFx with what we ordinarily call the z-component of a certain artificially invented vector. Although a torque is a twist on a plane, and it has no a priori vector character, mathematically it does behave like a vector. This vector is at right angles to the plane of the twist, and its length is proportional to the strength of the twist. The three components of such a quantity will transform like a real vector.
So we represent torques by vectors; with each plane on which the torque is supposed to be acting, we associate a line at right angles, by a rule. But “at right angles” leaves the sign unspecified. To get the sign right, we must adopt a rule which will tell us that if the torque were in a certain sense on the xy-plane, then the axis that we want to associate with it is in the “up” z-direction. That is, somebody has to define “right” and “left” for us. Supposing that the coordinate system is x, y, z in a right-hand system, then the rule will be the following: if we think of the twist as if we were turning a screw having a right-hand thread, then the direction of the vector that we will associate with that twist is in the direction that the screw would advance.
Why is torque a vector? It is a miracle of good luck that we can associate a single axis with a plane, and therefore that we can associate a vector with the torque; it is a special property of three-dimensional space. In two dimensions, the torque is an ordinary scalar, and there need be no direction associated with it. In three dimensions, it is a vector. If we had four dimensions, we would be in great difficulty, because (if we had time, for example, as the fourth dimension) we would not only have planes like xy, yz, and zx, we would also have tx-, ty-, and tz-planes. There would be six of them, and one cannot represent six quantities as one vector in four dimensions.
We will be living in three dimensions for a long time, so it is well to notice that the foregoing mathematical treatment did not depend upon the fact that x was position and F was force; it only depended on the transformation laws for vectors. Therefore if, instead of x, we used the x-component of some other vector, it is not going to make any difference. In other words, if we were to calculate axby−aybx, where a and b are vectors, and call it the z-component of some new quantity c, then these new quantities form a vector c. We need a mathematical notation for the relationship of the new vector, with its three components, to the vectors a and b. The notation that has been devised for this is c=a×b. We have then, in addition to the ordinary scalar product in the theory of vector analysis, a new kind of product, called the vector product. Thus, if c=a×b, this is the same as writing
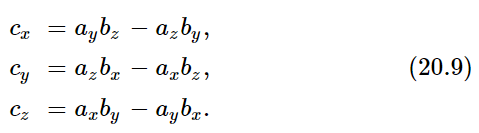
If we reverse the order of a and b, calling a, b and b, a, we would have the sign of c reversed, because cz would be bxay−byax. Therefore, the cross product is unlike ordinary multiplication, where ab=ba; for the cross product, b×a=−a×b. From this, we can prove at once that if a=b, the cross product is zero. Thus, a×a=0.
The cross product is very important for representing the features of rotation, and it is important that we understand the geometrical relationship of the three vectors a, b, and c. Of course, the relationship in components is given in Eq. (20.9) and from that one can determine what the relationship is in geometry. The answer is, first, that the vector c is perpendicular to both a and b. (Try to calculate c⋅a, and see if it does not reduce to zero.) Second, the magnitude of c turns out to be the magnitude of a times the magnitude of b times the sine of the angle between the two. In which direction does c point? Imagine that we turn a into b through an angle less than 180∘; a screw with a right-hand thread turning in this way will advance in the direction of c. The fact that we say a right-hand screw instead of a left-hand screw is a convention, and is a perpetual reminder that if a and b are “honest” vectors in the ordinary sense, the new kind of “vector” which we have created by a×b is artificial, or slightly different in its character from a and b, because it was made up with a special rule. If a and b are called ordinary vectors, we have a special name for them, we call them polar vectors. Examples of such vectors are the coordinate r, force F, momentum p, velocity v, electric field E, etc.; these are ordinary polar vectors. Vectors which involve just one cross product in their definition are called axial vectors or pseudo vectors. Examples of pseudo vectors are, of course, torque τ and the angular momentum L. It also turns out that the angular velocity ω is a pseudo vector, as is the magnetic field B.
In order to complete the mathematical properties of vectors, we should know all the rules for their multiplication, using dot and cross products. In our applications at the moment, we will need very little of this, but for the sake of completeness we shall write down all of the rules for vector multiplication so that we can use the results later. These are
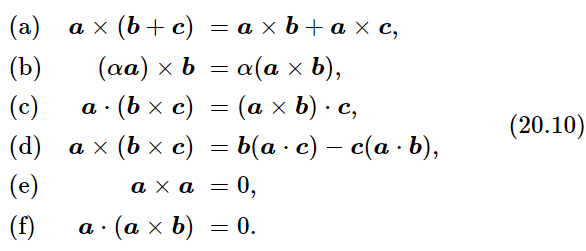



|
|
|
|
إجراء أول اختبار لدواء "ثوري" يتصدى لعدة أنواع من السرطان
|
|
|
|
|
|
|
دراسة تكشف "سببا غريبا" يعيق نمو الطيور
|
|
|
|
|
|
بالفيديوغراف: ممثل المرجعية الدينية العليا والامين العام للعتبة الحسينية يتفقدان مشروع مطار كربلاء الدولي
|
|
|
|
بالصور: سنابل تفيض بالخير في مزارع العتبة الحسينية (عمليات حصاد الحنطة)
|
|
|
|
تضمنت الجولة توجيهات متعلقة براحة المسافرين.. ممثل المرجعية العليا والامين العام للعتبة الحسينية يطلعان ميدانيا على سير العمل في مطار كربلاء الدولي
|
|
|
|
بالفيديو: مركز لعلاج العقم تابع للعتبة الحسينية يعلن عن أجراء (117) عملية تلقيح اصطناعي خلال الربع الاول من العام الحالي
|