


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-10-2015
Date: 14-10-2015
Date: 14-10-2015
|
The Egyptians had a writing system based on hieroglyphs from around 3000 BC. Hieroglyphs are little pictures representing words. It is easy to see how they would denote the word "bird" by a little picture of a bird but clearly without further development this system of writing cannot represent many words. The way round this problem adopted by the ancient Egyptians was to use the spoken sounds of words. For example, to illustrate the idea with an English sentence, we can see how "I hear a barking dog" might be represented by:
"an eye", "an ear", "bark of tree" + "head with crown", "a dog".
Of course the same symbols might mean something different in a different context, so "an eye" might mean "see" while "an ear" might signify "sound".
The Egyptians had a bases 10 system of hieroglyphs for numerals. By this we mean that they has separate symbols for one unit, one ten, one hundred, one thousand, one ten thousand, one hundred thousand, and one million.
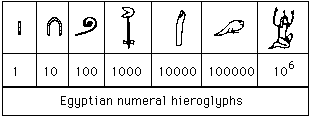
Here are the numeral hieroglyphs.
To make up the number 276, for example, fifteen symbols were required: two "hundred" symbols, seven "ten" symbols, and six "unit" symbols. The numbers appeared thus:

276 in hieroglyphs.
Here is another example:
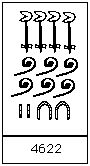
4622 in hieroglyphs.
Note that the examples of 276 and 4622 in hieroglyphs are seen on a stone carving from Karnak, dating from around 1500 BC, and now displayed in the Louvre in Paris.
As can easily be seen, adding numeral hieroglyphs is easy. One just adds the individual symbols, but replacing ten copies of a symbol by a single symbol of the next higher value. Fractions to the ancient Egyptians were limited to unit fractions (with the exception of the frequently used 2/3 and less frequently used 3/4). A unit fraction is of the form 1/n where n is an integer and these were represented in numeral hieroglyphs by placing the symbol representing a "mouth", which meant "part", above the number. Here are some examples:
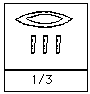
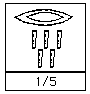
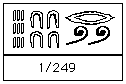
Notice that when the number contained too many symbols for the "part" sign to be placed over the whole number, as in 1/249 , then the "part" symbol was just placed over the "first part" of the number. [It was the first part for here the number is read from right to left.]
We should point out that the hieroglyphs did not remain the same throughout the two thousand or so years of the ancient Egyptian civilisation. This civilisation is often broken down into three distinct periods:
Old Kingdom - around 2700 BC to 2200 BC
Middle Kingdom - around 2100 BC to 1700 BC
New Kingdom - around 1600 BC to 1000 BC
Numeral hieroglyphs were somewhat different in these different periods, yet retained a broadly similar style.
Another number system, which the Egyptians used after the invention of writing on papyrus, was composed of hieratic numerals. These numerals allowed numbers to be written in a far more compact form yet using the system required many more symbols to be memorised. There were separate symbols for
1, 2, 3, 4, 5, 6, 7, 8, 9,
10, 20, 30, 40, 50, 60, 70, 80, 90,
100, 200, 300, 400, 500, 600, 700, 800, 900,
1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000
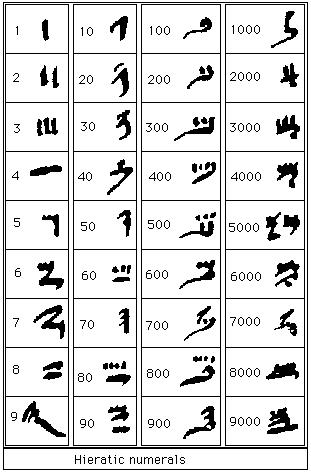
Here are versions of the hieratic numerals
With this system numbers could be formed of a few symbols. The number 9999 had just 4 hieratic symbols instead of 36 hieroglyphs. One major difference between the hieratic numerals and our own number system was the hieratic numerals did not form a positional system so the particular numerals could be written in any order.
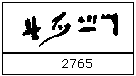
Here is one way the Egyptians wrote 2765 in hieratic numerals

Here is a second way of writing 2765 in hieratic numerals with the order reversed
Like the hieroglyphs, the hieratic symbols changed over time but they underwent more changes with six distinct periods. Initially the symbols that were used were quite close to the corresponding hieroglyph but their form diverged over time. The versions we give of the hieratic numerals date from around 1800 BC. The two systems ran in parallel for around 2000 years with the hieratic symbols being used in writing on papyrus, as for example in the Rhind papyrus and the Moscow papyrus, while the hieroglyphs continued to be used when carved on stone.
______________________________________________________________________________________________



|
|
|
|
هذه العلامة.. دليل على أخطر الأمراض النفسية
|
|
|
|
|
|
|
بالفيديو: بعثة الإغاثة الطبية التابعة للعتبة الحسينية في لبنان تقدم لاهالي صيدا المساعدات الطبية
|
|
|