


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-11-2021
Date: 11-9-2021
Date: 9-11-2021
|
The differential equation describing exponential growth is
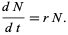 |
(1) |
This can be integrated directly
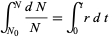 |
(2) |
to give
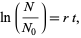 |
(3) |
where 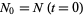 . Exponentiating,
. Exponentiating,
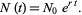 |
(4) |
This equation is called the law of growth and, in a much more antiquated fashion, the Malthusian equation; the quantity 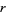 in this equation is sometimes known as the Malthusian parameter.
in this equation is sometimes known as the Malthusian parameter.
Consider a more complicated growth law
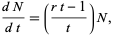 |
(5) |
where 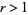 is a constant. This can also be integrated directly
is a constant. This can also be integrated directly
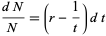 |
(6) |
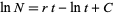 |
(7) |
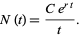 |
(8) |
Note that this expression blows up at 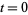 . We are given the initial condition that
. We are given the initial condition that 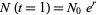 , so
, so 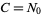 .
.
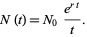 |
(9) |
The 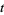 in the denominator of (◇) greatly suppresses the growth in the long run compared to the simple growth law.
in the denominator of (◇) greatly suppresses the growth in the long run compared to the simple growth law.
The (continuous) logistic equation, defined by
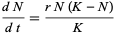 |
(10) |
is another growth law which frequently arises in biology. It has solution
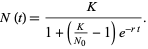 |
(11) |
REFERENCES:
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 290-295, 1999.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|