


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-10-2021
Date: 23-9-2021
Date: 21-12-2021
|
To predict the result of a measurement requires (1) a model of the system under investigation, and (2) a physical theory linking the parameters of the model to the parameters being measured. This prediction of observations, given the values of the parameters defining the model constitutes the "normal problem," or, in the jargon of inverse problem theory, the forward problem. The "inverse problem" consists in using the results of actual observations to infer the values of the parameters characterizing the system under investigation.
Inverse problems may be difficult to solve for at least two different reasons: (1) different values of the model parameters may be consistent with the data (knowing the height of the main-mast is not sufficient for calculating the age of the captain), and (2) discovering the values of the model parameters may require the exploration of a huge parameter space (finding a needle in a 100-dimensional haystack is difficult).
Although most of the formulations of inverse problems proceed directly to the setting of an optimization problem, it is actually best to start using a probabilistic formulation, the optimization formulation then appearing as a by-product.
Consider a manifold 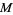 with a notion of volume. Then for any
with a notion of volume. Then for any 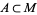 ,
,
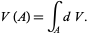 |
(1) |
A volumetric probability is a function 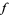 that to any
that to any 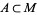 associates its probability
associates its probability
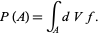 |
(2) |
If 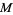 is a metric manifold endowed with some coordinates
is a metric manifold endowed with some coordinates 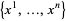 , then
, then
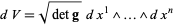 |
(3) |
and
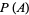 |
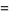 |
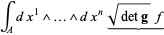 |
(4) |
 |
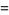 |
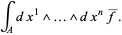 |
(5) |
(Note that the volumetric probability 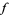 is an invariant, but the probability density
is an invariant, but the probability density 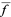 is not; it is a density.)
is not; it is a density.)
A basic operation with volumetric probabilities is their product,
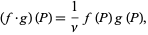 |
(6) |
where 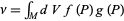 . This corresponds to a "combination of probabilities" well suited to many basic inference problems.
. This corresponds to a "combination of probabilities" well suited to many basic inference problems.
Consider an example in which two planes make two estimations of the geographical coordinates of a shipwrecked man. Let the probabilities be represented by the two volumetric probabilities 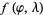 and
and 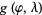 . The volumetric probability that combines these two pieces of information is
. The volumetric probability that combines these two pieces of information is
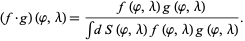 |
(7) |
This operation of product of volumetric probabilities extends to the following case:
1. There is a volumetric probability 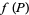 defined on a first manifold
defined on a first manifold  .
.
2. There is another volumetric probability  defined on a second manifold
defined on a second manifold 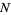 .
.
3. There is an application 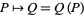 from
from 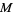 into
into 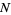 .
.
Then, the basic operation introduced above becomes
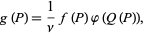 |
(8) |
where 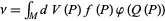 .
.
In a typical inverse problem, there is:
1. A set of model parameters 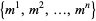 .
.
2. A set of observable parameters 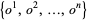 .
.
3. A relation 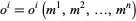 predicting the outcome of the possible observations.
predicting the outcome of the possible observations.
The model parameters are coordinates on the model parameter manifold 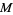 while the observable parameters are coordinates over the observable parameter manifold
while the observable parameters are coordinates over the observable parameter manifold 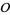 . When the points on
. When the points on 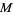 are denoted
are denoted 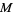 ,
,  , ... and the points on
, ... and the points on 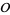 are denoted
are denoted 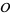 ,
, 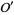 , ..., the relation between the model parameters an the observable parameters is written
, ..., the relation between the model parameters an the observable parameters is written 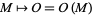 .
.
The three basic elements of a typical inverse problem are:
1. Some a priori information on the model parameters, represented by a volumetric probability 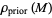 defined over
defined over 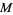 .
.
2. Some experimental information obtained on the observable parameters, represented by a volumetric probability 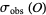 defined over
defined over 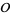 .
.
3. The 'forward modeling' relation 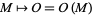 that we have just seen.
that we have just seen.
The use of equation (8) leads to
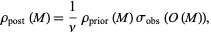 |
(9) |
where  is a normalization constant. This volumetric probability represents the resulting information one has on the model parameters (obtained by combining the available information). Equation (9) provides the more general solution to the inverse problem. Common methods (Monte Carlo, optimization, etc.) can be seen as particular uses of this equation.
is a normalization constant. This volumetric probability represents the resulting information one has on the model parameters (obtained by combining the available information). Equation (9) provides the more general solution to the inverse problem. Common methods (Monte Carlo, optimization, etc.) can be seen as particular uses of this equation.
Considering an example from sampling, sample the a priori volumetric probability 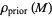 to obtain (many) random models
to obtain (many) random models 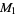 ,
, 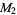 , .... For each model
, .... For each model 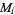 , solve the forward modeling problem,
, solve the forward modeling problem, 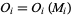 . Give to each model
. Give to each model 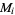 a probability of 'survival' proportional to
a probability of 'survival' proportional to 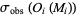 . The surviving models
. The surviving models  ,
,  , ... are samples of the a posteriori volumetric probability
, ... are samples of the a posteriori volumetric probability
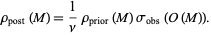 |
(10) |
Considering an example from least-squares fitting, the model parameter manifold may be a linear space, with vectors denoted 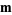 ,
,  , ..., and the a priori information may have the Gaussian form
, ..., and the a priori information may have the Gaussian form
![rho_(prior)(m)=kexp[-1/2(m-m_(prior))^(T)C_m^(-1)(m-m_(prior))].](https://mathworld.wolfram.com/images/equations/InverseProblem/NumberedEquation9.gif) |
(11) |
The observable parameter manifold may be a linear space, with vectors denoted 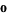 ,
, 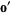 , ... and the information brought by measurements may have the Gaussian form
, ... and the information brought by measurements may have the Gaussian form
![sigma_(obs)(o)=kexp[-1/2(o-o_(obs))^(T)C_o^(-1)(o-o_(obs))]).](https://mathworld.wolfram.com/images/equations/InverseProblem/NumberedEquation10.gif) |
(12) |
The forward modeling relation becomes, with these notations,
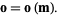 |
(13) |
Then, the posterior volumetric probability for the model parameters is
![rho_(post)(m)=kexp[-S(m)],](https://mathworld.wolfram.com/images/equations/InverseProblem/NumberedEquation12.gif) |
(14) |
where the misfit function 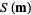 is the sum of squares
is the sum of squares
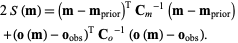 |
(15) |
The maximum likelihood model is the model 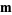 maximizing
maximizing 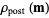 . It is also the model minimizing
. It is also the model minimizing 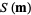 . It can be obtained using a quasi-Newton algorithm,
. It can be obtained using a quasi-Newton algorithm,
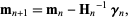 |
(16) |
where the Hessian of 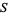 is
is
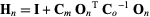 |
(17) |
and the gradient of 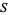 is
is
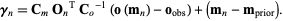 |
(18) |
Here, the tangent linear operator 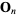 is defined via
is defined via
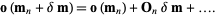 |
(19) |
As we have seen, the model 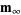 at which the algorithm converges maximizes the posterior volumetric probability
at which the algorithm converges maximizes the posterior volumetric probability 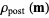 .
.
To estimate the posterior uncertainties, one can demonstrate that the covariance operator of the Gaussian volumetric probability that is tangent to 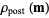 at
at 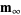 is
is 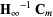 .
.
REFERENCES:
Groetsch, C. W. Inverse Problems: Activities for Undergraduates. Washington, DC: Math. Assoc. Amer., 1999.
Kozhanov, A. I. Composite Type Equations and Inverse Problems. Utrecht, Netherlands: VSP, 1999.
Mosegaard, K. and Tarantola, A. "Probabilistic Approach to Inverse Problems." In International Handbook of Earthquake & Engineering Seismology, Part A. New York: Academic Press, pp. 237-265, 2002.
Prilepko, A. I.; Orlovsky, D. G.; and Vasin, I. A. Methods for Solving Inverse Problems in Mathematical Physics. New York: Dekker, 1999.
Tarantola, A. Inverse Problem Theory and Model Parameter Estimation. Philadelphia, PA: SIAM, 2004. http://www.ccr.jussieu.fr/tarantola/.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|